Textbook Section 8.2: Conservative and Non-Conservative Forces

Section 8.1: Conservative Forces

The amount of work done on an object only depends on where it started and where it ended; it does not depend on the path you took from the initial to final place. Bouncing a book up and down before putting it back on the shelf might make you think you’re expending energy, but according to physics, no net work has been done on the book if it ended up where it started. Forces that work this way (only depend on initial and final points, not the path between) are called conservative forces. Gravity, other forms of potential energy (such as spring forces) are conservative forces. Friction is an example of a non-conservative force; because friction depends on how much contact you have had with the ground, the longer the path means the more energy is lost to fiction.

Section 8.2: Spring Potential Energy

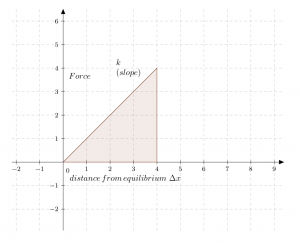
As you stretch a string away from its equilibrium position (the position it returns to when not stretched or compressed) you must continually add energy to the system. At first, the spring stretches easily, but the longer it gets, the larger the required force to stretch it further. While still a conservative system (you put energy into the spring to compress it, which is then transferred to another object when released), it’s not a constant force relationship. For this reason, the area under the curve is a triangle, not a rectangle, and the work done on the spring is given by

The force needed to stretch a spring is given by , where is the spring constant (a constant value for each spring, small if the spring is easy to stretch and large if the spring is stiff, given in units of ) and or is the distance the spring is compressed or stretched away from its equilibrium position (a of zero means the spring is in equilibrium).

The potential energy stored in a spring by extending or compressing it some distance is given by

The force required to stretch a spring some distance is given by

We now have yet another conservative energy term to add to our conservation of energy equation. Because all the energy we have initially must be all the energy we have at the end (simply transformed into different forms), we can add spring potential energy to the equation to get

where is the initial extension of the spring and is the final extension of the spring. Note that when using the above equation, we are talking about two distinct moments in time, initial and final. Everything on the left happens at the initial moment, everything on the right happens at the final moment. If a type of energy is not changing, you can cancel it from both sides (for example, object is not moving at beginning or end — cancel ; no springs are involved — cancel ; object does not change height — cancel ).

Section 8.3: Calculating Non-Conservative Forces

Textbook Section 8.3: Conservation

Non-conservative forces are forces that rely on the path you took, and include friction and drag forces. The amount of work done by a non-conservative force, , is calculated as the frictional force applied times the distance over which the frictional force acts, or

This is the final term (for this chapter) that we will add to our conservation of energy equation. Remember that work is defined as , so that the work done by friction opposing the motion of the object will always include a negative sign from the cos term. Thus, the work done by a non-conservative force must be added to (and in effect, subtracted from) the left side of the equation, giving us

Section 8.4: Power

Textbook Section 7.4: Power

Power is the rate at which work is done, and is calculated as

in units of Watts (W) which is equivalent to 1 W = 1 J/s. Another common unit of power is horsepower, where 1 hp = 746 W. We often encounter power when talking about the amount of power or electricity used by electrical appliances. For example, a light bulb might be rated at 60 Watts. What does this mean? It means that the bulb consumes 60 W, or 60 J/s, of power in order to work. The energy used over time can be given by , or the power rating of the bulb (60 J/s) times the amount of time you leave it on for (say an , or 3,600 sec), giving us an energy usage of 60 J/s 3,600 s = 216,000 J. A kilowatt hour (kWh) is a measure of energy, not power, and is equal to 3.6 J.

In Class Group Problem 8.1:

You have a 5.0 kg block of wood pressed against a spring ( = 40 N/m) as shown below. You push back the block to compress the spring by 3.0 cm, then let go. Assume the table is frictionless. How fast is the block moving 3 seconds after you let go?

In Class Group Problem 8.2:

In the previous question, let’s now consider what happens if friction is present. Assume that the coefficient of kinetic friction between the block and the table is = 0.350. How far does the block move before coming to a rest? Solve using conservation of energy and non-conservative forces.

In Class Group Problem 8.3:

You release a 12 kg box from rest at the top of an incline. The incline is 6.0 m long and inclined at 15 from the horizontal. The coefficient of kinetic friction between the box and the incline is = 0.034. How fast is the box moving when it reaches the bottom of the incline? Solve using energy and non-conservative forces.

In Class Group Problem 8.4:

A 0.500 kg block rests on a horizontal surface with = 0.230. The block is pressed into a spring with = 1,250 N/m, compressing the spring by 3.0 cm. The block is then released, slides 5.0 cm across the surface, and partway up an incline at 22 with the same as the surface.

Find the maximum height the block reaches before turning around.

How fast is the block moving when it reaches half its maximum height?

In Class Group Problem 8.5:

At the train station, you notice a large horizontal spring at the end of the track where the train comes in. This is a safety device to stop the train so that it will not go plowing through the station if the engineer misjudges the stopping distance. While waiting, you wonder what would be the fastest train that the spring could stop when fully compressed to 3.0 ft. To keep the passengers safe as possible when the spring stops the train, you assume that the maximum stopping acceleration of the train, caused by the spring, is . You make a guess that the train might have a mass of 0.5 million kilograms. Assume all frictional forces are negligible.

In Class Group Problem 8.6:

The Navy wants a new airplane launcher for their aircraft carriers and you are on the design team. The launcher is effectively a large spring that pushes the plane for the first 5 meters of the 20 meter long runway. During that same time, the plane’s jet engines supply a constant thrust of 5.4 N for the entire length of the runway. The 2000 kg planes need to have a velocity of 45 m/s by the end of the runway. The coefficient of friction between the tires of the plane and the runway is zero over the first 5 meters (when the spring is in contact with the plane) and then 0.4 for the last 15 meters of the runway. What should be the spring constant for the launcher?

In Class Group Problem 8.7:

You are the technical advisor to the Dave Letterman Show. Your task is to design a circus stunt in which Super Dave Osbourne, who weighs 170 pounds, is shot out of a cannon that is elevated 40 from the horizontal. The “cannon” is actually a 3-foot diameter tube that uses a stiff spring and a puff of smoke rather than explosives to launch Super Dave. The manual for the cannon states that the spring constant is 1820 Newtons/meter. The spring is compressed by a motor until its free end is level with the bottom of the cannon tube, which is 5 feet above the ground. A small seat is attached to the free end of the spring for Super Dave to sit on. When the spring is released, it extends 9 feet up into the tube. Neither the seat nor the chair touch the sides of the 9-foot long tube. After a drum roll, the spring is released and Super Dave will fly through the air with the appropriate sound effects and smoke. You have an airbag 3-feet thick for Super Dave to land on. You know that the airbag will exert an average force of 2850 Newtons in all directions. You need to determine if this airbag is thick enough to stop Super Dave safely — that is, so he has slowed to a stop before hit reaches the ground.

Practice Exam Question 8.1:

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

Amazon has hired you to help design their new distribution center. They have a ramp they will use to slide boxes from one area to another, and want you to determine the coefficient of kinetic friction between the boxes and the ramp. The ramp has an incline of 15 to the horizontal, and boxes are placed at rest at the top of the 6.5 m-long ramp. You accidentally left your phone at home this morning, so you can’t time how long it takes the boxes to reach the bottom of the ramp. However, you do have a spring lying around that you know has a spring constant of = 8,500 N/m. You place a 35 kg box at the top of the ramp. The box accelerates down the ramp and hits the spring at the bottom, compressing the spring by 17 cm before coming to a stop. What is the coefficient of kinetic friction between the ramp and the box?

Practice Exam Question 8.2:

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

A block of mass 4.0 kg is pushed back against a spring with a spring constant of 15,000 N/m. The spring is initially compressed by 8.5 cm. Once released from the spring, the box slides 1.5 m across the floor horizontally and then encounters a ramp at an incline of 22. If the coefficient of kinetic friction between the block and the floor is 0.120 and the coefficient of kinetic friction between the block and the incline is 0.090, how far vertically up the incline will the box slide before coming to a stop and beginning to slide back down?