There are two main scenarios in which waves break; either far from shore in the deep ocean or as they reach the shore. We’ll begin by discussing waves far from shore, since we have been focused on deep water most of this chapter, and then will shift gears to consider how waves interact with the shoreline.

Waves Far from the Shore

It’s likely that you’ve observed waves breaking at the shore, as we are lucky to teach and learn on a campus that abuts the bay. Some of you may have also seen breaking waves away from the shore, whether that be while driving over the Mt Hope Bridge or from the deck of a boat. So what causes these waves to break? When the crest of an ocean waves reaches an unstable condition it spills down the front of the wave, creating a turbulent wake whose intensity decreases with distance downstream, and producing white capping from the entrainment of air.

Our ability to predict when and where a wave will break remains an open area of research. There are a variety of mathematical models based on differing environmental parameters, as well as thresholds. Here we’ll explore a short list of models, designed not be to exhaustive, but rather give you an appreciation for the diversity of models.

Some models use wave height and period as the criteria for predicting when a wave will break. For example, Michel (1893) proposed the following inequality relating wave height, H, to gravity, g, and wave period, T.

Similarly, Ochi and Tsai (1983), presented a model that differs from Michel’s with a slight adjustment to the value of the coefficient.

Others have proposed criteria based on the vertical acceleration of water particles to predict when a wave with break. These include a model by Phillips (1953),

and another less conservative equation from Longuet-Higgens (1977) that reduces the coefficient multiplied with gravity,

Work by Miche (1944) suggests that wave height, wavelength, and water depth should all be considered when predicting whether or not a wave will break, given by the expression

Unlike all the other models, Miche’s work introduces the consideration of water depth, which brings us to a different discussion entirely. How does the interaction of waves with the sea floor influence wave breaking?

Waves at the Shore

Most of the waves discussed in this chapter refer to deep water waves in the open ocean. But what happens when these waves move towards shore and encounter shallow water? Remember that in deep water, a wave’s speed depends on its wavelength, but in shallow water wave speed depends on the depth. When waves approach the shore they will “touch bottom” at a depth equal to half of their wavelength; in other words, when the water depth equals the depth of the wave base (Figure 8.3.1). At this point their behavior will begin to be influenced by the bottom.

When the wave touches the bottom, friction causes the wave to slow down. As one wave slows down, the one behind it catches up to it, thus decreasing the wavelength. However, the wave still contains the same amount of energy, so while the wavelength decreases, the wave height increases. Eventually the wave height exceeds 1/7 of the wavelength, and the wave becomes unstable and forms a breaker. Often breakers will start to curl forwards as they break. This is because the bottom of the wave begins to slow down before the top of the wave, as it is the first part to encounter the seafloor. So the crest  of the wave gets “ahead” of the rest of the wave, but has no water underneath it to support it (Figure 8.3.2).

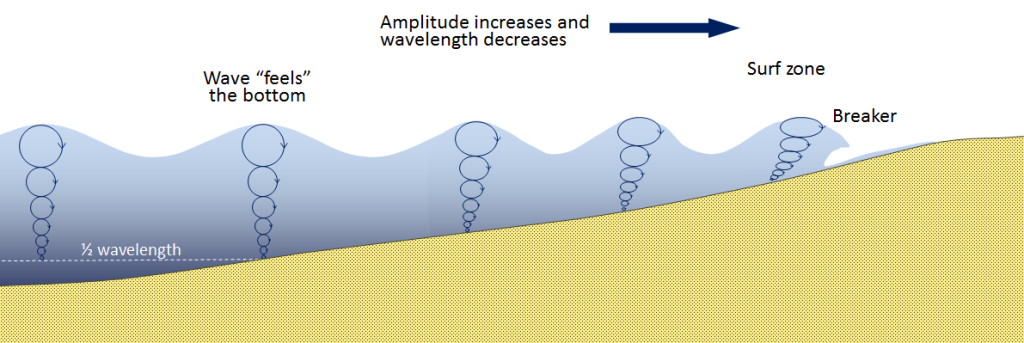
There are three main types of breakers: spilling, plunging, and surging. These are related to the steepness of the bottom, and how quickly the wave will slow down and its energy will get dissipated.

• Spilling breakers form on gently sloping or flatter beaches, where the energy of the wave is dissipated gradually. The wave slowly increases in height, then slowly collapses on itself (Figure 8.3.3). For surfers, these waves provide a longer ride, but they are less exciting.

• Plunging breakers form on more steeply-sloped shores, where there is a sudden slowing of the wave and the wave gets higher very quickly. The crest outruns the rest of the wave, curls forwards and breaks with a sudden loss of energy (Figure 8.3.4). These are the “pipeline” waves that surfers seek out.

• Surging breakers form on the steepest shorelines. The wave energy is compressed very suddenly right at the shoreline, and the wave breaks right onto the beach (Figure 8.3.5). These waves give too short (and potentially painful) a ride for surfers to enjoy.

Many models have also been proposed to predict when waves with break close to shore, including McCowan’s equation from 1894, which relates wave height to water depth, given by

More recently, Battjes (2000) proposed a more complex model that relies on water depth, as well as gravity, and wave period. 

These two models for predicting when waves with break close to shore is by no means an exhaustive list. Rather, it is meant to shine light on the range of models — from very simple, to quite complex — across a long span of history. Our ability to predict when waves will break close to shore, and away from shore, remains an active area of research today.

Wave Refraction

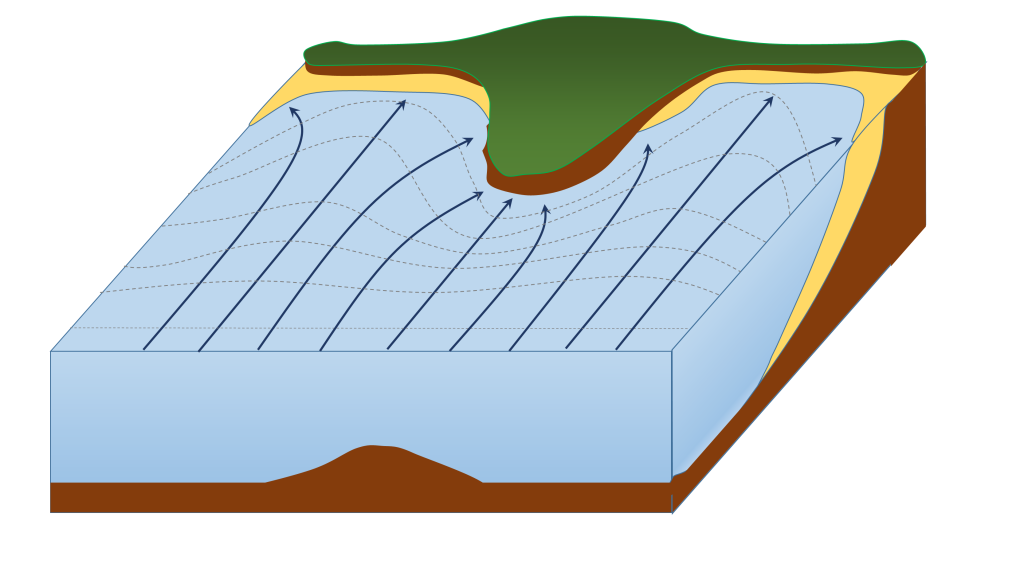
Swell can be generated anywhere in the ocean and therefore can arrive at a beach from almost any direction. But if you have ever stood at the shore you have probably noticed that the waves usually approach the shore somewhat parallel to the coast. This is due to wave refraction. If a wave front approaches shore at an angle, the end of the wave front closest to shore will touch bottom before the rest of the wave. This will cause that shallower part of the wave to slow down first, while the rest of the wave that is still in deeper water will continue on at its regular speed. As more and more of the wave front encounters shallower water and slows down, the wave font refracts and the waves tend to align themselves nearly parallel to the shoreline (they are refracted towards the region of slower speed). The fact that the waves do not arrive perfectly parallel to the beach causes longshore currents and longshore transport that run parallel to the shore.

Refraction can also explain why waves tend to be larger off of points and headlands, and smaller in bays. A wave front approaching shore will touch the bottom off of the point before it touches bottom in a bay. Once again, the shallower part of the wave front will slow down, and cause the rest of the wave front to refract towards the slower region (the point). Now all of the initial wave energy is concentrated in a relatively small area off of the point, creating large, high energy waves (Figure 8.3.6). In the bay, the refraction has caused the wave fronts to refract away from each other, dispersing the wave energy, and leading to calmer water and smaller waves. This makes the large waves of a “point break” ideal for surfing, while water is calmer in a bay, which is where people would launch a boat. This difference in wave energy also explains why there is net erosion on points, while sand and sediments get deposited in bays.

References

Miche, R. 1944. Mouvements ondulatoires de l’océan pour une eau profonde constante et décroissante. Annales des Ponts et Chaussées 114: 369-406.

Michel, J. 1893. The highest waves in water. Philos Mag; 36:430–7.

Ochi, M, Tsai, C. 1983. Prediction of occurrence of breaking waves in deep water. J Phys Oceanogr; 13(11):2008–19

Phillips, O. 1958. The equilibrium range in the spectrum of wind-generated waves. J Fluid Mech; 4:785–90.

Longuet-Higgins, M. 1969. On wave breaking and equilibrium spectrum of wind-generated waves. Proc R Soc Lond Ser A; 310:151–9.

McCowan, J. 1894. On the highest wave of permanent type. Philosophical Magazine, 38:351-357.

Hallowell, S., Myers, A. T. and Arwade, S. R. 2015 Variability of breaking wave characteristics and impact loads on offshore wind turbines supported by monopiles. Wind Energy. DOI: 10.1002/we.1833