Modeling the interaction between fluids and solid bodies is an inherently challenging task due to the complex coupling of the two systems. When the fluid moves, it can induce motion in the body, either through translation or rotation, or both. As the body moves within the fluid, it alters the pressure fields, velocities, and accelerations of the flow, which, in turn, affects the body once again. This creates a cyclical problem—much like the age-old question of “which came first, the chicken or the egg?”—as each element influences the other. The challenge lies in determining where to begin the calculation and when to stop. In this chapter, we will explore different approaches for modeling fluid-body interactions by categorizing the loads, linearizing the problem, and identifying opportunities for simplification.

Hydrodynamic loads can be categorized in several ways, depending on the nature of the forces involved. Here’s we’ll use the framework shown in Figure 9.2.2. A useful distinction is between static loads and dynamic loads. This categorization will help us understand the different types of forces at play and the appropriate methods for modeling them.

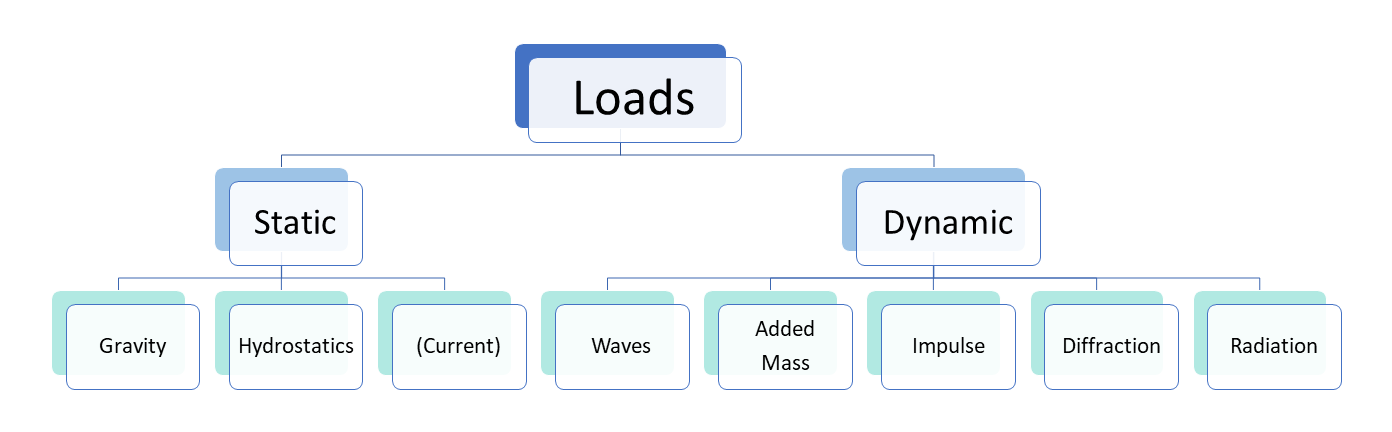
Static Loads

Static loads include forces that do not involve motion of the fluid or the body. These loads are typically time-invariant and include gravity and hydrostatic forces. In some cases, current may be treated as a static load, despite the fact that water is moving. The treatment of current as a static load is a simplification where we assume it to be time-invariant and approximate it with a mean value.

Hydrostatics

Hydrostatics: Hydrostatic forces arise when a body is submerged in a fluid at rest. The pressure at any point within the fluid is determined by the depth, as given by:

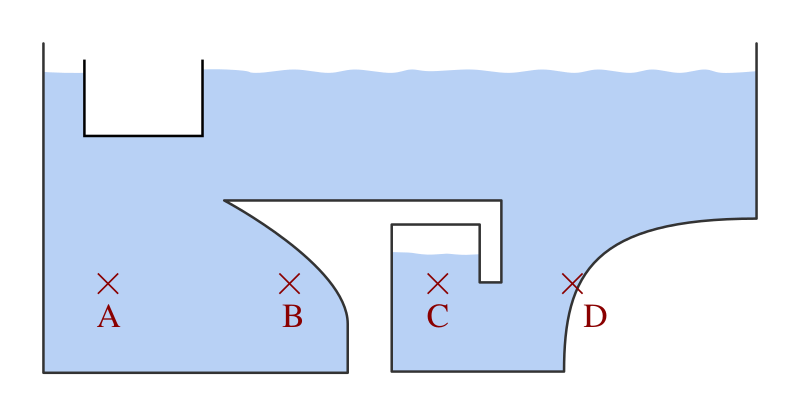
where is the fluid density (kg/m³), g is gravity (m/s²), and h is distance (m) from the surface, given pressure units of N/m² or Pa. This means that at any position with the same h value, the hydrostatic pressure will be the same, as illustrated by points A, B, C, and D in Figure 9.2.2. Points sitting above A, B, C, or D would have lower hydrostatic pressures because their distance from the surface is smaller. Points deeper in the water, or sitting below A, B, C, and D would have higher hydrostatic pressures.

The focus of this chapter is hydrodynamic loads, which are forces not pressures. Force has units of Newtons (N) while pressure has units Pascals (Pa) equivalent to a Newton per square meter (N/m²). So it is easy to compute a force from a pressure by simply multiplying by a surface area.

where F is force (N), P is pressure (Pa), and A is area (m²).

For a body at rest, the sum of hydrostatic forces pushing upwards must be balanced by the force due to gravity in the downwards direction. If the forces are not in balance than the body will not be at rest. This is given mathematically as follows,

This can be further deconstructed mathematically, to match Figure 9.2.4 below, as,

where is the fluid density (kg/m³), V is the volume of the body or displaced fluid (m³), and g is gravity.

Current Loads

Ocean currents, which are driven by factors such as wind, tides, or pressure gradients, exert forces on bodies within the fluid. Though current involves the movement of fluid over time, we often approximate it as a static load by assuming it to be constant over the time scale of interest:

In reality, current can lead to dynamic loads, particularly in the form of vibrational forces caused by vortex shedding. These dynamic effects will be discussed later in this chapter.

Dynamic Loads

Dynamic loads involve forces resulting from the motion of either the fluid, the body, or both. These loads are typically more complex than static loads and vary with time. The interaction of waves with bodies is the primary source of dynamic hydrodynamic forces, and these effects are significantly influenced by the wave environment, the body’s characteristics, and their relative motion.

Dynamic loads include, but are not limited to, effects from waves, added mass, impulse, diffraction, and radiation. It is worth noting that these loads are not always fully independent, such that a Venn diagram may serve as a better schematic of their overlapping nature. Because there are a wider variety of dynamic loads, and that they tend to be more complex, we will begin to elaborate upon them in this section and will continue to explore them through the rest of this chapter.

When considering bodies in the ocean, we need to consider both the object and the fluid. Many questions are introduced. How large is the body? What are the environmental conditions? Are there waves, if so, what size? Current? Tides? And in what ways do the body and the environment interact? How do they compare with one another in terms of scale?

Wave-Induced Loads: The motion of waves can cause a range of dynamic effects on bodies, including reflection, refraction, diffraction, and radiation. These effects depend on the size, shape, and motion of the body, as well as the characteristics of the waves.

• Diffraction refers to the scattering of waves when they encounter an object, altering the wave patterns around the body.
• Radiation describes the forces generated by the waves that are created by a moving body.

The magnitude of these effects depends on several factors, including the body’s size, shape, and motion relative to the waves.

Distinguishing Between Small and Large Bodies: When modeling wave-body interactions, the size of the body relative to the wave characteristics is a key factor. For example, when considering vertical circular cylinders (e.g., offshore platforms), the ratio of the body’s diameter ($D$) to the wave’s wavelength ($\lambda$) and wave amplitude ($A$) can help categorize the interaction:

• When the characteristic size of the body is small relative to the wavelength, inertia forces dominate, and diffraction is minimal.
• As the body size increases and becomes comparable to the wavelength, diffraction effects become more pronounced, and inertia forces become less significant.

For vertical circular cylinders, for example, this distinction is made by comparing the structure’s size, D, to the characteristic wavelength, , and wave amplitude, A. When $kD$ is small and A/D is large, the body is classified as small. In this case, vortex shedding and flow separation dominate, while diffraction is negligible because the body has little impact on the wave field. On the other hand, when $kD$ is larger than order one and A/D is small, diffraction becomes significant, and separation is minimal. The regions of dominant wave loading regimes are outlined in Table 9.2.1 below, adapted from Sarpkaya.

Table 9.2.1 Wave loading regimes for vertical circular cylinders. (Adapted from Sarpkaya.)

Dominant Regime	Range
Inertia
Small drag, large inertia
Comparable drag and inertia
Diffraction

References

Sarpkaya, Turgut. Wave Forces on Offshore Structures. Cambridge University Press, Cambridge, 2010.