3. Loads on Slender Bodies

Maija Benitz

3. Loads on Slender Bodies

Morison’s equation

Morison’s equation, named after the researchers Morison, O’Brien, Johnson, and Schaaf who published it in 1950, is a widely used formulation for calculating the hydrodynamic loading on offshore structures, particularly slender bodies such as vertical cylinders that extend above the water surface. This empirically derived equation provides a method for predicting the forces acting on a body in an oscillating fluid flow, with two terms: one for drag forces and another for inertial forces. Although Morison’s equation has limitations, it remains a valuable tool for estimating loading in oscillatory flow conditions, especially when detailed pressure distributions are difficult to model.

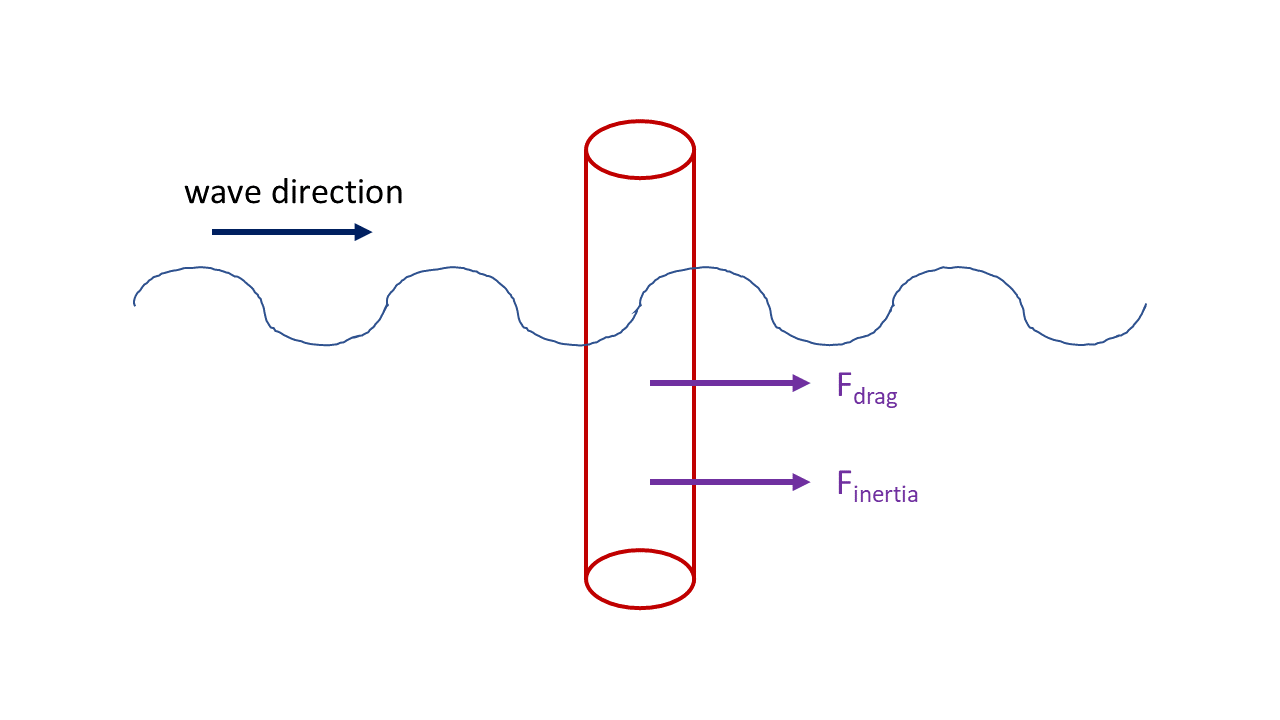
**Figure 9.3.1** A vertical, slender cylinder, piercing the free surface with waves traveling from left to right. The forces due to drag and inertia act in the same direction as the wave propagation. Morison’s equation can be used to predict the resulting loads from this wave-body interaction.

Hydrodynamic loads in the direction of wave propagation for stationary slender objects in waves are modeled with the Morison’s equation using,

$F_{inline} = \frac{1}{2} \rho C_d A_p |U|U + \rho C_m V_0 \frac{dU}{dt}$

where

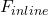$F_{inline}$ is the force acting on the body in the direction of wave propagation,
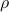$\rho$ is the fluid density,
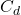$C_d$ is the drag coefficient,
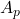$A_p$ is the frontal cross-sectional area of the body,
U is the fluid velocity,
$\frac{dU}{dt}$ is the fluid acceleration,
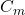$C_m$ is the inertia coefficient,
$V_0$ is the displaced volume of the object.

The first term in Morison’s equation captures the drag effects proportional to the square of the velocity and the second term is comprised of inertial loads in phase with the flow acceleration. Note that in the first term, an absolute value is placed around the first U to maintain the sign (or direction) of the fluid velocity.

Selection of drag and inertia terms is very important to predicting accurate hydrodynamic loads. As such, these coefficients are given an entire section of this chapter.

Limitations of Morison’s Equation

While Morison’s equation provides a practical means for calculating the forces on slender bodies, it has several limitations:

Lift forces: The equation does not account for fluctuating lift forces that may arise, such as those generated by vortex shedding.
Inline force prediction: The equation does not always accurately predict the inline force on the body, particularly in complex wave conditions.
Memory effects: Morison’s equation neglects the memory effects of the fluid, meaning it does not fully capture the time-dependent interaction between the body and the fluid.
Complex wave kinematics: Ocean waves are difficult to model accurately due to factors like current-wave separation, omnidirectional wave propagation, and turbulence. The discrepancies between predicted and measured forces often stem from these complexities, as well as the limitations of the equation itself.

Despite these limitations, Morison’s equation is still effective for estimating the forces on small offshore structures in oscillating flow, where detailed simulations of the fluid dynamics would otherwise be too computationally expensive or complex.

Froude-Krylov force

The previous section focused on stationary slender bodies. If the body is freely moving in waves, the hydrodynamic loads are slightly different. This can be treated with a slight modification to the Morison’s equation by adding a term. Now, the force in the wave direction can be predicted with

$F_{inline} = \frac{1}{2} \rho C_d A_p |U|U + \rho C_m V_0 \frac{dU}{dt} + \rho V_0 \dot U$

where the new term includes density, $\rho$ , displaced volume, $V_0$ , and $\dot U$ is the fluid acceleration, as the dot indicates a derivative with respect to time.

This new term is called the Froude-Krylov force. It is the result neglecting wave scattering to represent the pressure field around the vertical cylinder more simply. According to the Froude-Krylov Hypothesis, for a sufficiently small body, the pressure field is unaffected by the incident waves, allowing diffraction effects to be ignored. The Froude-Krylov force represents the force that would act on the body as if it were absent, meaning the body does not alter the surrounding flow field.

Morison’s equation offers a straightforward way to calculate the forces on small structures, where determining pressure distributions due to complex flow and vortices would otherwise be challenging. Similarly, the Froude-Krylov force provides a simple approach when diffraction is ignored. However, if the flow remains attached to the structure, it becomes easier to calculate the pressure field that generates the forces on the body. For larger structures, where the flow remains attached and the incident waves scatter off the surface, the assumptions behind Morison’s equation no longer hold.

Added Mass

In addition to drag and inertial forces, the added mass effect can play a significant role in the hydrodynamic response of bodies moving through a fluid.

The concept of added mass was first observed by Friedrich Wilhelm Bessel in 1828 during experiments with spherical pendulums. He found that the oscillation period of a pendulum increased when submerged in water compared to air, an effect attributed to the additional mass of fluid displaced by the moving body.

When a body accelerates or decelerates in a fluid, it moves a volume of fluid along with it. Although the total mass of the system remains constant, the presence of this displaced fluid alters the acceleration of the body and changes the system’s inertia. This phenomenon is referred to as added mass or added inertia.

The added mass moment of inertia in a viscous fluid exists only briefly after an acceleration or deceleration of the fluid or a transition from a steady to an unsteady state. These effects are present before flow separation and viscous forces become significant and are limited to small displacements of the body.

To illustrate the impact of added mass on a system undergoing simple harmonic motion, consider the equation of motion for a body subjected to a driving force:

$m \ddot x + b \dot x + k x = f(t)$

m is the mass,
b is the damping constant,
k is the spring constant,
x is the displacement of the body,
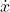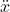$\dot x$ and $\ddot x$ represented velocity and acceleration, respectively,
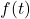$f(t)$ is the driving force.

To include the effects of added mass, an additional term is included, as follows,

$m \ddot x + b \dot x + k x = f(t) - m_a \ddot x$

where $m_a$ is the added mass. This can be rearranged to show

$(m + m_a) \ddot x + b \dot x + k x = f(t)$

where the two masses are lumped together. So, where the system’s natural frequency is given by,

$\omega_n = \sqrt{\frac{k}{m}}$

when the effects of added mass are included, it becomes

$\omega_n = \sqrt{\frac{k}{m+m_a}}$

Now that the denominator is larger, the natural frequency decreases and the period grows larger, just as Bessel observed in 1828.

Conclusion

Morison’s equation and the associated concepts of drag, inertia, and added mass provide essential tools for predicting the forces acting on offshore structures in oscillatory flow. While Morison’s equation is effective in many scenarios, its limitations highlight the challenges of accurately modeling wave-body interactions. As the size and complexity of the structure increase, more detailed models may be necessary to capture the full range of hydrodynamic effects.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License