6.  Impact Loads

Maija Benitz

6. Impact Loads

In Chapter 8, we introduced the concept of breaking waves, exploring both offshore and nearshore wave breaking. Predicting when a wave will break is inherently complex, and numerous numerical models attempt to define the breaking threshold using a range of parameters.

**Figure 9.6.1** A breaking wave at the shore in Porto Covo, Portugal (Photo by Alvegaspar, [CC-BY-SA-4.0], Wikimedia Commons).

We now extend the wave breaking discussion by considering the forces generated when waves break on structures. These forces, known as impact loads or slamming loads, are short-lived but can reach very large magnitudes. Understanding and predicting these loads requires knowledge of breaking wave characteristics, forces generated by the wave impact, and the system’s dynamic response.

Challenges in Predicting Slamming Loads

Calculating impact loads is complicated due to two main sources of uncertainty:

Variability in Wave Breaking: Breaking wave characteristics—such as wave height, water depth, wavelength, wave period, and seabed slope—are highly variable.
Limitations of Engineering Models: Current engineering models have limitations in accurately predicting the loads from breaking waves, which can affect the structural reliability of offshore applications.

**Figure 9.6.2.** Visualization of a breaking wave approaching shore. The distance between the still water line (SWL) and the breaking wave height is given by eta_B.

Errors in predicting loads can lead to significant design risks. If impact loads are underestimated, the resulting structures (such as ships, oil platforms, and offshore wind turbines) may fail under extreme wave conditions, creating safety hazards and environmental risks.

The concern is that the following chain of events could occur: (1) design loads are calculated with current models that underestimate the real impact of breaking waves; (2) structures based on these underestimated loads are built, potentially in large numbers; (3) extreme wave events bring breaking waves that exceed the design loads, causing widespread structural failures. Such failures would create significant environmental concerns and hinder public support for a variety of types of offshore projects.

Modeling Wave Slamming Loads

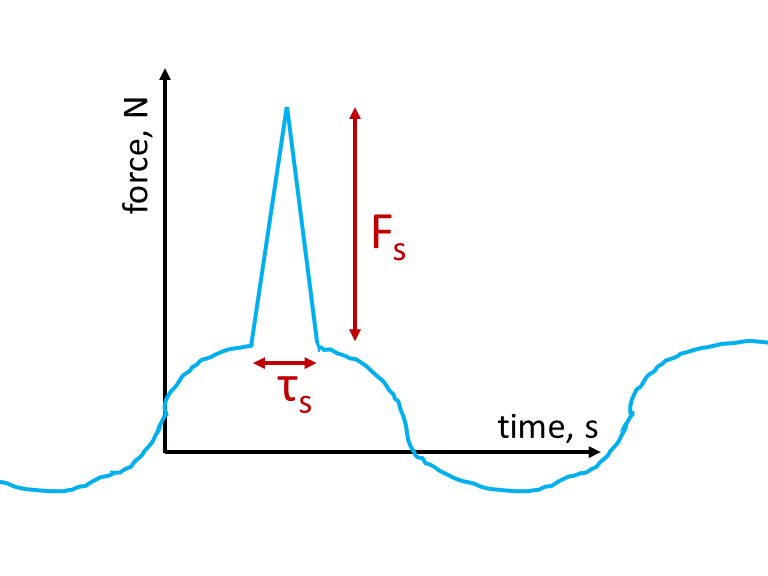
To account for wave slamming, an additional term is often added to Morison’s equation to capture the effects of the high-impact force. Figure 9.6.3 illustrates a wave slamming load as a sudden spike added to the typical wave load profile. The peak force magnitude, denoted $F_s$ , occurs over a short time period, $\tau_s$ .

**Figure 9.6.3** Graphical representation of a wave slamming load. A sinusoidal curve represents loads from regular waves and a large spike is shown where the wave breaks. F_s is the size of the wave slamming load that occurs over a short time period, tau_s.

The modified Morison’s equation that includes wave slamming is:

$F_{\text{total}} = F_{\text{drag}}+ F_{\text{inertia}} + F_{\text{slamming}}$

where $F_{\text{slamming}}$ (or $F_s$ ) accounts for the slamming force. The wave slamming force is further detailed here,

$F_{\text{slamming}} = F_s = \frac{1}{2} \rho C_s D c_B^2 \lambda \eta_B$

where:

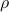$\rho$ (kg/m³) is density,
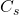$C_s$ is the wave slamming coefficient,
D (m) is the body diameter,
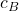$c_B$ (m/s) is the breaking wave celerity (aka speed),
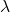$\lambda$ is the curling factor, and
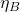$\eta_B$ (m) is the breaking wave height above the still water line (SWL).

Wave Slamming Coefficient

Like other coefficients in Morison’s equation, the slamming coefficient, $C_s$ , is a dimensionless value. It depends on parameters like wave front steepness, depth of immersion, impact duration, and curling factor.

There is a wide range in $C_s$ values, and studies have shown that Morison’s equation often underestimates slamming loads because it doesn’t fully capture fluid-structure interactions, such as wave run-up on the structure. Three formulations for $C_s$

Goda, 1966

$C_s = \pi (1-\frac{ct}{R})$

Campbell-Weynberg, 1980

$C_s = 5.15 (\frac{2R}{2R+19ct} + \frac{0.107ct}{2R})$

Wienke-Oumerachi, 2005

$C_s = 2 \pi - 2 \sqrt{\frac{ct}{R}}(tanh^{-1}(\sqrt{1-\frac{ct}{R}}))$

In each of these models, c is celerity, t is time, and R is radius.

The differences among these models highlight the range of approaches in modeling slamming loads and the empirical nature of these equations, as evidenced by complex mathematical formulations like inverse hyperbolic functions.

Summary

Impact loads from breaking waves are challenging to model due to their short duration and high magnitude, as well as the variability in wave breaking characteristics. Despite numerous empirical models for slamming loads, this area remains active in research due to its importance in designing reliable offshore structures.

References

Hallowell, S., Myers, A. T., and Arwade, S. R. (2016) Variability of breaking wave characteristics and impact loads on offshore wind turbines supported by monopiles. Wind Energ., 19: 301–312. doi: 10.1002/we.1833.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License