6. Cylindrical and Spherical Coordinates
The Cartesian coordinate system provides a straightforward way to describe the location of points in space. Some surfaces, however, can be difficult to model with equations based on the Cartesian system. This is a familiar problem; recall that in two dimensions, polar coordinates often provide a useful alternative system for describing the location of a point in the plane, particularly in cases involving circles. In this section, we look at two different ways of describing the location of points in space, both of them based on extensions of polar coordinates. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such as calculating the volume of a round water tank or the amount of oil flowing through a pipe. Similarly, spherical coordinates are useful for dealing with problems involving spheres, such as finding the volume of domed structures.
Cylindrical Coordinates
When we expanded the traditional Cartesian coordinate system from two dimensions to three, we simply added a new axis to model the third dimension. Starting with polar coordinates, we can follow this same process to create a new three-dimensional coordinate system, called the cylindrical coordinate system. In this way, cylindrical coordinates provide a natural extension of polar coordinates to three dimensions.
Definition
In the cylindrical coordinate system, a point in space (Figure 3.6.1) is represented by the ordered triple (r,θ,z), where
- (r,θ) are the polar coordinates of the point’s projection in the xy-plane
- z is the usual z-coordinate in the Cartesian coordinate system
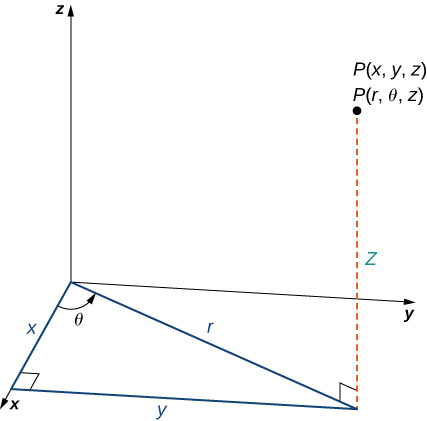
In the xy-plane, the right triangle shown in Figure 3.6.2 provides the key to transformation between cylindrical and Cartesian, or rectangular, coordinates.
Theorem
Conversion between Cylindrical and Cartesian Coordinates
The rectangular coordinates (x,y,z) and the cylindrical coordinates (r,θ,z) of a point are related as follows:

As when we discussed conversion from rectangular coordinates to polar coordinates in two dimensions, it should be noted that the equation ![]() has an infinite number of solutions. However, if we restrict θ to values between 0 and 2π, then we can find a unique solution based on the quadrant of the xy-plane in which original point (x,y,z) is located. Note that if x=0, then the value of θ is either π/2, 3π/2, or 0, depending on the value of y.
has an infinite number of solutions. However, if we restrict θ to values between 0 and 2π, then we can find a unique solution based on the quadrant of the xy-plane in which original point (x,y,z) is located. Note that if x=0, then the value of θ is either π/2, 3π/2, or 0, depending on the value of y.
Notice that these equations are derived from properties of right triangles. To make this easy to see, consider point P in the xy-plane with rectangular coordinates (x,y,0) and with cylindrical coordinates (r,θ,0), as shown in the following figure.
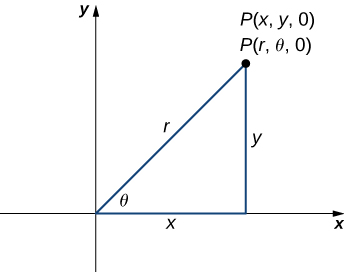
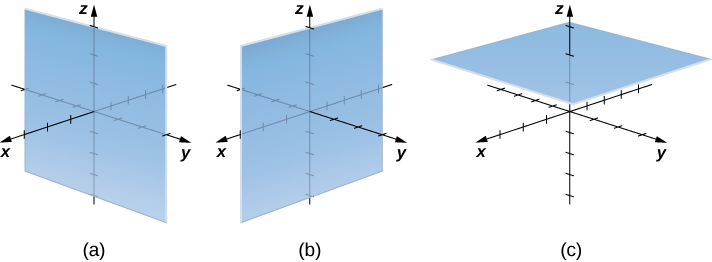
Let’s consider the differences between rectangular and cylindrical coordinates by looking at the surfaces generated when each of the coordinates is held constant. If c is a constant, then in rectangular coordinates, surfaces of the form x=c, y=c, or z=c are all planes. Planes of these forms are parallel to the yz-plane, the xz-plane, and the xy-plane, respectively. When we convert to cylindrical coordinates, the z-coordinate does not change. Therefore, in cylindrical coordinates, surfaces of the form z=c are planes parallel to the xy-plane. Now, let’s think about surfaces of the form r=c. The points on these surfaces are at a fixed distance from the z-axis. In other words, these surfaces are vertical circular cylinders. Last, what about θ=c? The points on a surface of the form θ=c are at a fixed angle from the x-axis, which gives us a half-plane that
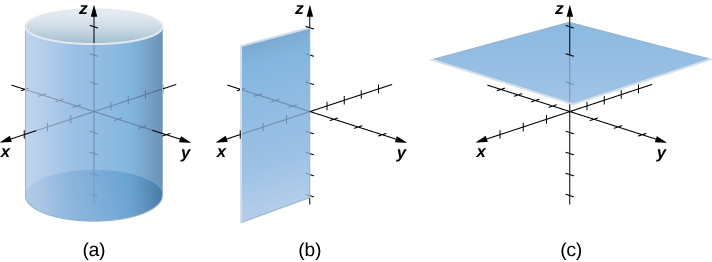
Example: Converting from Cylindrical to Rectangular Coordinates
Plot the point with cylindrical coordinates (4,2π/3,-2) and express its location in rectangular coordinates.
Solution
Conversion from cylindrical to rectangular coordinates requires a simple application of the equations listed in the Conversion between Cylindrical and Cartesian Coordinates theorem from above:
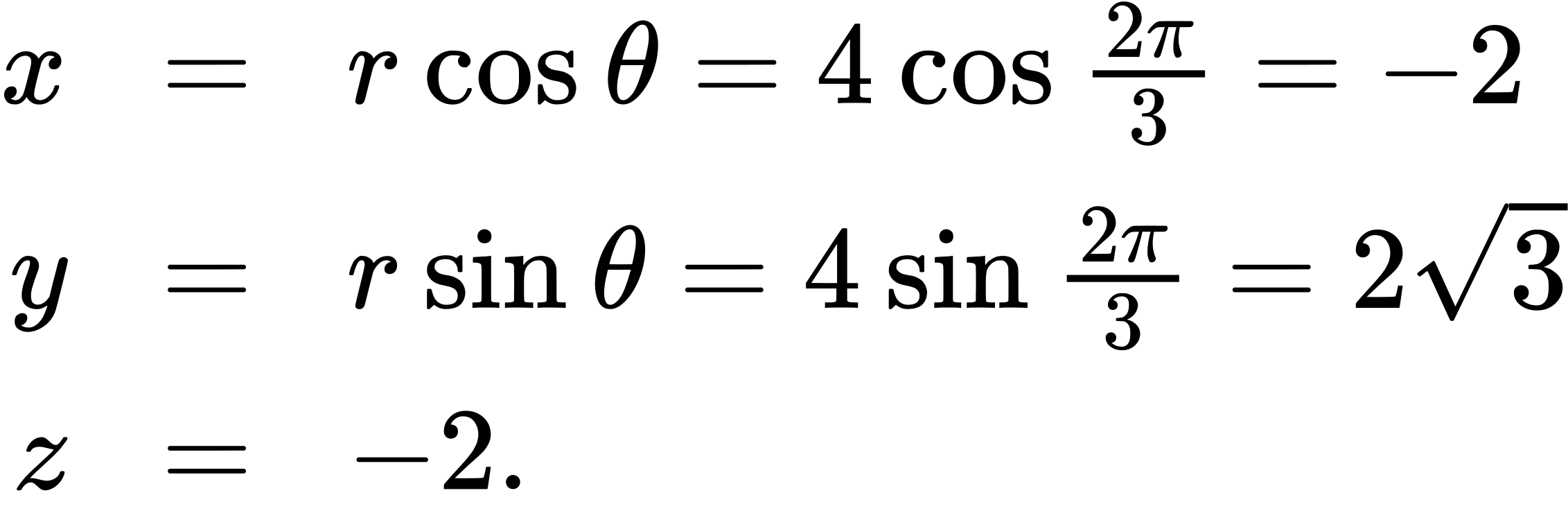
The point with cylindrical coordinates (4, 2 ![]() /3, -2) has rectangular coordinates (-2,2
/3, -2) has rectangular coordinates (-2,2![]() ,-2) (see the following figure).
,-2) (see the following figure).
The use of cylindrical coordinates is common in fields such as physics. Physicists studying electrical charges and the capacitors used to store these charges have discovered that these systems sometimes have a cylindrical symmetry. These systems have complicated modeling equations in the Cartesian coordinate system, which make them difficult to describe and analyze. The equations can often be expressed in more simple terms using cylindrical coordinates. For example, the cylinder described by equation
Example: Identifying Surfaces in the Cylindrical Coordinate System
Describe the surfaces with the given cylindrical equations.
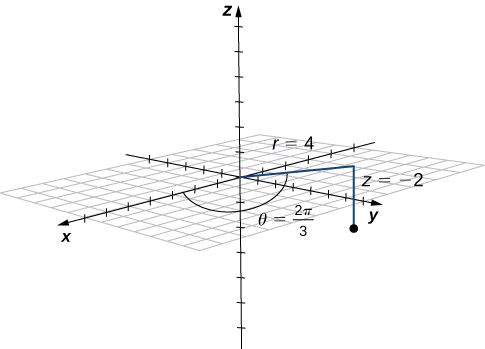
- θ=π/4
- r2+z2=9
- z=r
Solution
(1) When the angle θ is held constant while r and z are allowed to vary, the result is a half-plane (see the following figure).
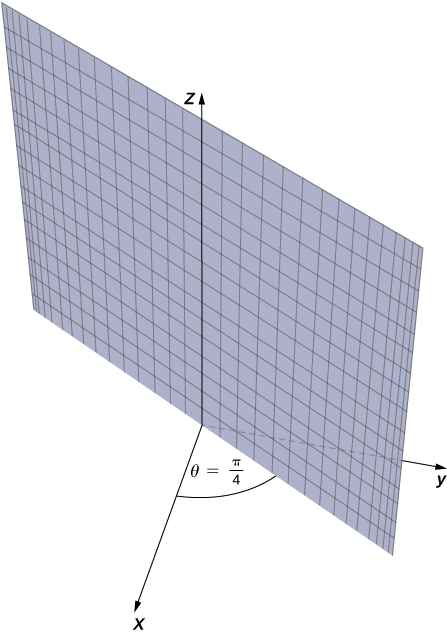
(2) Substitute r2=x2+y2into equation r2+z2=9 to express the rectangular form of the equation: x2+y2+z2=9. This equation describes a sphere centered at the origin with radius 3 (see the following figure).
(3) To describe the surface defined by equation z=r, is it useful to examine traces parallel to the xy-plane. For example, the trace in plane z=1 is circle r=1, the trace in plane z=3 is circle r=3, and so on. Each trace is a circle. As the value of z increases, the radius of the circle also increases. The resulting surface is a cone (see the following figure).
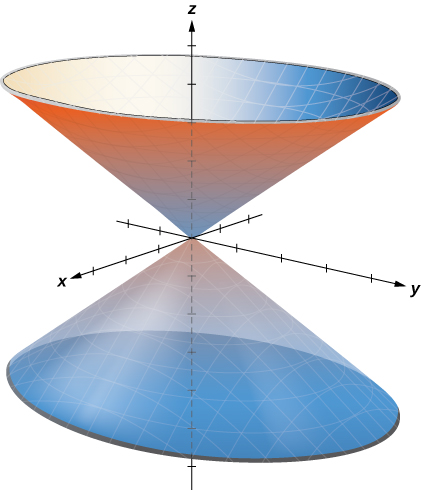
Spherical Coordinates
In the Cartesian coordinate system, the location of a point in space is described using an ordered triple in which each coordinate represents a distance. In the cylindrical coordinate system, location of a point in space is described using two distances (r and z) and an angle measure (θ). In the spherical coordinate system, we again use an ordered triple to describe the location of a point in space. In this case, the triple describes one distance and two angles. Spherical coordinates make it simple to describe a sphere, just as cylindrical coordinates make it easy to describe a cylinder. Grid lines for spherical coordinates are based on angle measures, like those for polar coordinates.
Definition
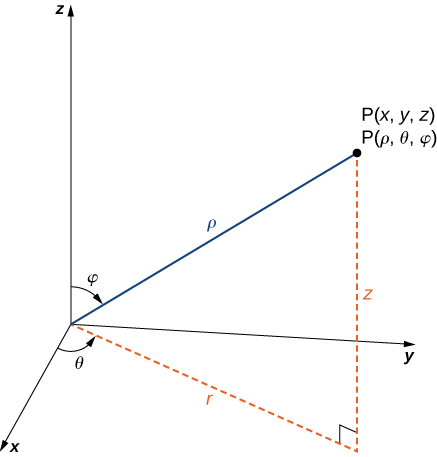
In the spherical coordinate system, a point P in space (Figure 3.6.5) is represented by the ordered triple (ρ,θ,φ) where
- ρ (the Greek letter rho) is the distance between P and the origin ρ≠0;
- θ is the same angle used to describe the location in cylindrical coordinates;
- φ (the Greek letter phi) is the angle formed by the positive z-axis and line segment OP—, where O is the origin and 0≤φ≤π.
By convention, the origin is represented as (0,0,0) in spherical coordinates.
Theorem
Converting among Spherical, Cylindrical, and Rectangular Coordinates Rectangular coordinates (x,y,z) and spherical coordinates (ρ,θ,φ) of a point are related as follows:

If a point has cylindrical coordinates (r,θ,z), then these equations define the relationship between cylindrical and spherical coordinates.

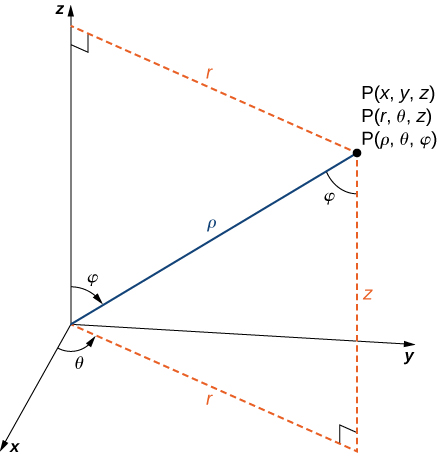
The formulas to convert from spherical coordinates to rectangular coordinates may seem complex, but they are straightforward applications of trigonometry. Looking at Figure 3.6.6, it is easy to see that r=ρ sin φ. Then, looking at the triangle in the xy-plane with r as its hypotenuse, we have x=r cos θ=ρ sin φ cos θ. The derivation of the formula for y is similar. Figure 3.6.5 also shows that ρ2=r2+z2=x2+y2+z2 and z=ρ cos φ. Solving this last equation for φ and then substituting ρ=r2+z2 (from the first equation) yields φ=arccos ![]() Also, note that, as before, we must be careful when using the formula tan θ=y/x to choose the correct value of θ.
Also, note that, as before, we must be careful when using the formula tan θ=y/x to choose the correct value of θ.
As we did with cylindrical coordinates, let’s consider the surfaces that are generated when each of the coordinates is held constant. Let c be a constant, and consider surfaces of the form ρ=c. Points on these surfaces are at a fixed distance from the origin and form a sphere. The coordinate θ in the spherical coordinate system is the same as in the cylindrical coordinate system, so surfaces of the form θ=c are half-planes, as before. Last, consider surfaces of the form φ=c.
The points on these surfaces are at a fixed angle from the z-axis and form a half-cone (Figure 3.6.7).
Example: Converting from Spherical Coordinates
Plot the point with spherical coordinates (8,π/3,π/6) and express its location in both rectangular and cylindrical coordinates.
Solution
Use the equations in Converting among Spherical, Cylindrical, and Rectangular Coordinates theorem shown above to translate between spherical and cylindrical coordinates:
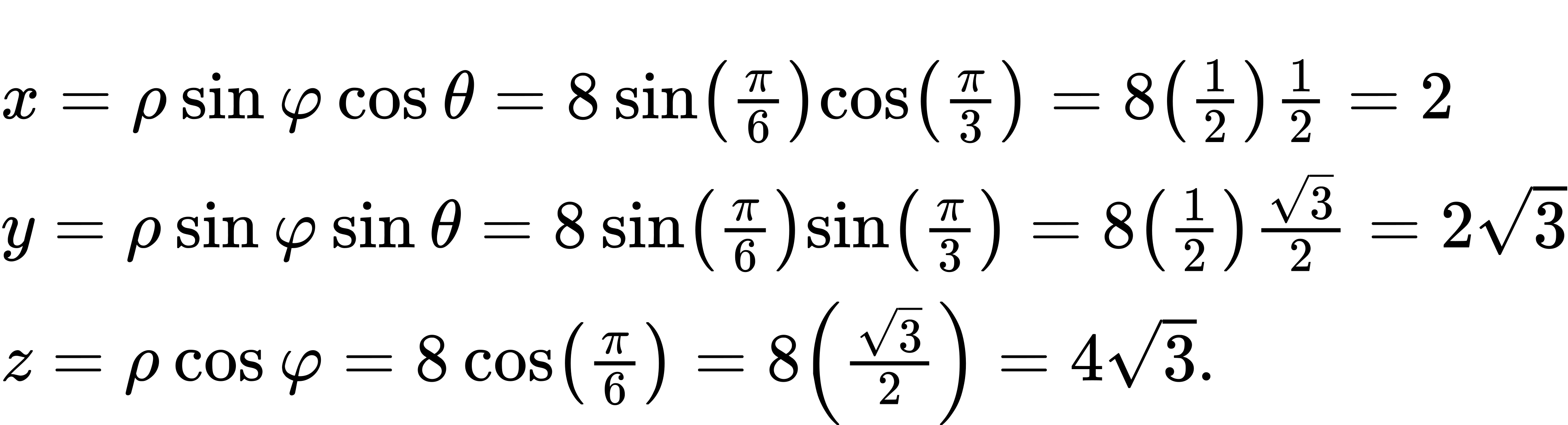
The point with spherical coordinates (8,π/3,π/6) has rectangular coordinates (2,2 ![]() ). Finding the values in cylindrical coordinates is equally straightforward:
). Finding the values in cylindrical coordinates is equally straightforward:
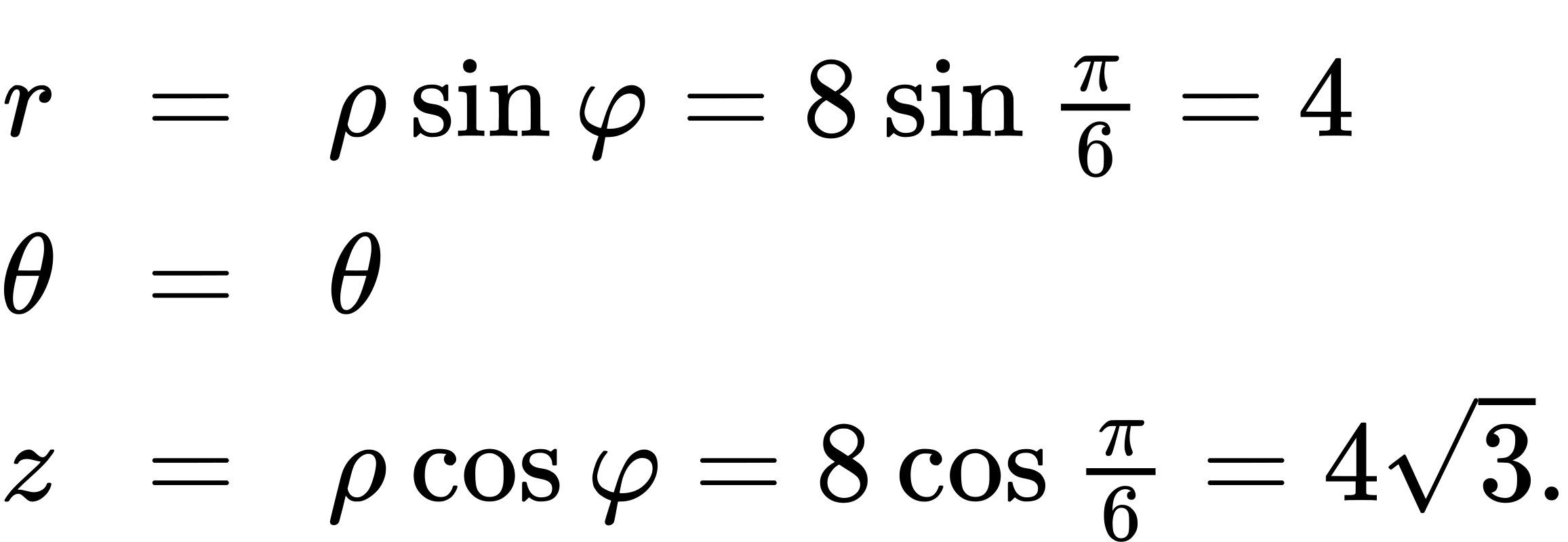
Thus, cylindrical coordinates for the point are (4,π/3,4![]() ).
).
Spherical coordinates are useful in analyzing systems that have some degree of symmetry about a point, such as the volume of the space inside a domed stadium or wind speeds in a planet’s atmosphere. A sphere that has Cartesian equation x2+y2+z2=c2 has the simple equation ρ=c in spherical coordinates.
In geography, latitude and longitude are used to describe locations on Earth’s surface, as shown in Figure 3.6.8. Although the shape of Earth is not a perfect sphere, we use spherical coordinates to communicate the locations of points on Earth. Let’s assume Earth has the shape of a sphere with radius 4000 mi. We express angle measures in degrees rather than radians because latitude and longitude are measured in degrees.
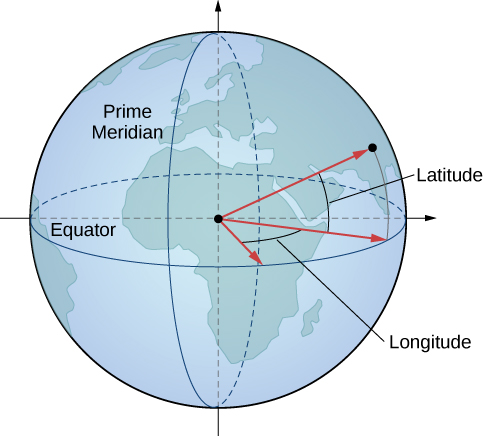
Let the center of Earth be the center of the sphere, with the ray from the center through the North Pole representing the positive z-axis. The prime meridian represents the trace of the surface as it intersects the xz-plane. The equator is the trace of the sphere intersecting the xy-plane.
Cylindrical and spherical coordinates give us the flexibility to select a coordinate system appropriate to the problem at hand. A thoughtful choice of coordinate system can make a problem much easier to solve, whereas a poor choice can lead to unnecessarily complex calculations. In the following example, we examine several different problems and discuss how to select the best coordinate system for each one.
Example: Choosing the Best Coordinate System
In each of the following situations, we determine which coordinate system is most appropriate and describe how we would orient the coordinate axes. There could be more than one right answer for how the axes should be oriented, but we select an orientation that makes sense in the context of the problem. Note: There is not enough information to set up or solve these problems; we simply select the coordinate system.
- Find the center of gravity of a bowling ball.
- Determine the velocity of a submarine subjected to an ocean current.
- Calculate the pressure in a conical water tank.
- Find the volume of oil flowing through a pipeline.
- Determine the amount of leather required to make a football.

Solution
- Clearly, a bowling ball is a sphere, so spherical coordinates would probably work best here. The origin should be located at the physical center of the ball. There is no obvious choice for how the x-, y– and z-axes should be oriented. Bowling balls normally have a weight block in the center. One possible choice is to align the z-axis with the axis of symmetry of the weight block.
- A submarine generally moves in a straight line. There is no rotational or spherical symmetry that applies in this situation, so rectangular coordinates are a good choice. The z-axis should probably point upward. The x– and y-axes could be aligned to point east and north, respectively. The origin should be some convenient physical location, such as the starting position of the submarine or the location of a particular port.
- A cone has several kinds of symmetry. In cylindrical coordinates, a cone can be represented by equation z=kr, where k is a constant. In spherical coordinates, we have seen that surfaces of the form φ=c are half-cones. Last, in rectangular coordinates, elliptic cones are quadric surfaces and can be represented by equations of the form
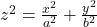 . In this case, we could choose any of the three. However, the equation for the surface is more complicated in rectangular coordinates than in the other two systems, so we might want to avoid that choice. In addition, we are talking about a water tank, and the depth of the water might come into play at some point in our calculations, so it might be nice to have a component that represents height and depth directly. Based on this reasoning, cylindrical coordinates might be the best choice. Choose the z-axis to align with the axis of the cone. The orientation of the other two axes is arbitrary. The origin should be the bottom point of the cone.
. In this case, we could choose any of the three. However, the equation for the surface is more complicated in rectangular coordinates than in the other two systems, so we might want to avoid that choice. In addition, we are talking about a water tank, and the depth of the water might come into play at some point in our calculations, so it might be nice to have a component that represents height and depth directly. Based on this reasoning, cylindrical coordinates might be the best choice. Choose the z-axis to align with the axis of the cone. The orientation of the other two axes is arbitrary. The origin should be the bottom point of the cone. - A pipeline is a cylinder, so cylindrical coordinates would be best the best choice. In this case, however, we would likely choose to orient our z-axis with the center axis of the pipeline. The x-axis could be chosen to point straight downward or to some other logical direction. The origin should be chosen based on the problem statement. Note that this puts the z-axis in a horizontal orientation, which is a little different from what we usually do. It may make sense to choose an unusual orientation for the axes if it makes sense for the problem.
- A football has rotational symmetry about a central axis, so cylindrical coordinates would work best. The z-axis should align with the axis of the ball. The origin could be the center of the ball or perhaps one of the ends. The position of the x-axis is arbitrary.

