3. Basic Commands
To get started writing code in MATLAB, several commands are essential to begin to operate the program. A command is a basic instruction that the user gives the program. These instructions, if given correctly, cause MATLAB to output a response such as printing a solution to a problem, executing a step in a larger process, or relaying information about the code. This chapter details several common commands which will frequently be used when writing scripts. The MATLAB user interface includes a command window designed specifically to facilitate the user executing simple commands or interacting with specific parts of larger codes, which will be addressed in the discussion of scripts. The command window and commands as a concept are fundamental concepts for coding. As a result, the following chapter has been written to instruct users on the variety, effects, and syntax required for command use in the broader context of MATLAB.
Arithmetic in MATLAB
MATLAB is a well-versed tool for completing simple mathematical operations or solving algebraic equations. To complete these operations, the user must be aware of the notation that is required for the computer to understand what was input.
General Operations
To complete addition, subtraction, multiplication, or division the user must be precise with how they write their expressions. The included image depicts how to properly input operations. The first thing the user should be mindful of is the lack of an equal sign in mathematical operations. MATLAB uses single equal signs to assign a value to a variable, which is not what we want to do when solving an expression. Instead, press enter without typing an equal sign to tell MATLAB to solve the expression. Note that operations do not depend on if spaces are present between the numerical values and the operator. For multiplication and division note the use of an asterisk (
want to do when solving an expression. Instead, press enter without typing an equal sign to tell MATLAB to solve the expression. Note that operations do not depend on if spaces are present between the numerical values and the operator. For multiplication and division note the use of an asterisk (*) and a forward slash (/) as their respective operators. Several operations can be done by inputting values with consideration of conventional order of operations rules (think the acronym PEMDAS for parenthesis, exponents, multiplication, division, addition, and subtraction if you forget).
Exponents and roots can be calculated in a similar manner in MATLAB. To compute an operation with an exponent, use a caret (^) followed by the value of the power. To compute roots, the same notation can be used with the root depicted as an exponent. For example, four squared could be written as 4^2 in MATLAB and the square root of four could be written as either 4^(1/2). The sqrt function can also be written using the sqrt() function, with all values which would be under the radical being contained within the parenthesis.
Calculating expressions using logarithms and exponentials are easy using MATLAB as well. To calculate a base 10 logarithm, use the function “log(x)” with x being the numerical value of the logarithm. In a similar manner, values taken to a power of e can be written using “exp(x)”, which would be input as “exp(4)” in MATLAB.
Trigonometry in MATLAB
MATLAB defaults to using radians to calculate degrees, which requires the user to be careful when entering angles to ensure the value is not calculated incorrectly. The functions degree() and radian() can be used to convert between an angle in degrees and an angle in radians. When computing trigonometry operations such as sin() or cos() in MATLAB, the alternative function sind(), cosd(), or tand() can be used to inform MATLAB that the value entered in the trigonometry operation is in degrees. This saves the user the need to convert between radians and degrees.
Basic Statistics
Often we store and/or create large matrices of values in MATLAB and it can be useful to determine various statistical properties of these large data sets. There are two especially helpful commands for determining the size of a vector or matrix, which are length() and size(). The minimum and maximum value can be easily computed with the min() and max() commands. The mean (or average) can be calculated with mean(), noting that average() is not a built-in command in MATLAB. The standard deviation command is std().
Complex Expressions
MATLAB can calculate complex expressions in the same manner as simple expressions. MATLAB, like any traditional calculator, calculates specifically based on what the user inputs. While expressions are input using the same formatting regardless of their complexity, it is increasingly important to consider the order of operations that the system will use as a result of parenthesis or the lack thereof placed by the user. To get a feel for typing complex expressions within MATLAB’s command window, review the following examples and reproduce them within MATLAB yourself.
Examples
The following examples demonstrate how to input complex expressions into the command window.
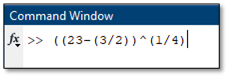


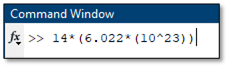

The Display Command (disp)
The display command (typed “disp”) allows the user to instruct the program to display a message in the command window. The display command is an excellent way to give instructions or other information in the command window for the user of the code. This can include instructions about the code’s function that appear when the user runs the code, greetings for the user, error messages, or conclusions determined by the code.
The display command appears in the following format in MATLAB. To use the display command, type disp followed by a set of parentheses with single quotations inside of them. Everything else in the quotations will be displayed in the command window by the program.
disp (‘Message Here.’)
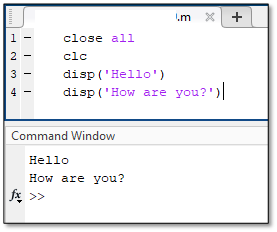 Note that the message being displayed cannot contain apostrophes, as the code will stop reading the message there. Additionally, it is important to understand that this command is not the best way to prompt users to input data or other information into the code, as the input command is best suited for that function.
Note that the message being displayed cannot contain apostrophes, as the code will stop reading the message there. Additionally, it is important to understand that this command is not the best way to prompt users to input data or other information into the code, as the input command is best suited for that function.
The Input Command (input)
The input function, typed input, operates as a way for the user to assign a value to a variable. With the input command, the user can have MATLAB provide a prompt in the command window. The user is then able to respond to the prompt by entering in their input directly after the prompt in the command window. An example of the input command is to the right. The user would type their response where the yellow box is next to the prompt. Note that the variable x will be assigned the user input for the remainder of the code unless another function reassigns its value.
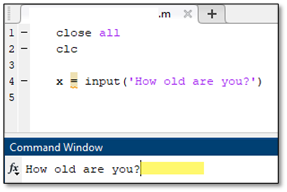
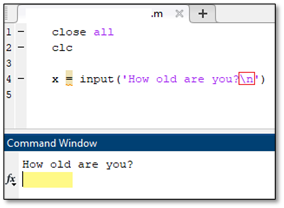 To improve the appearance of this function the user can add \n to the command, which will cause everything following the symbol to appear in the next line. If added to the end of the display command, as shown in the second example, the prompt to type an input appears in the line below the text in the command window and not next to the text, as indicated by the yellow box in the image. This is an easy way to improve the appearance and usability of a code, which will ensure data is properly input and that the user easily operates the code.
To improve the appearance of this function the user can add \n to the command, which will cause everything following the symbol to appear in the next line. If added to the end of the display command, as shown in the second example, the prompt to type an input appears in the line below the text in the command window and not next to the text, as indicated by the yellow box in the image. This is an easy way to improve the appearance and usability of a code, which will ensure data is properly input and that the user easily operates the code.
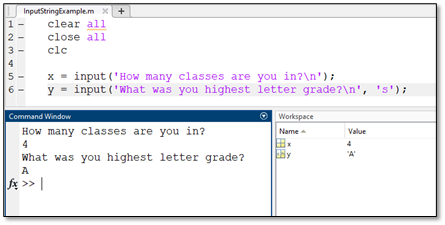
The method of using the input command introduced is designed for inputs that are strictly numeric. There are many applications where the user would like to input a value that is not a number and instead is letters or words. Many programming languages refer to a series of characters that consist of letters as “strings”. MATLAB follows this convention and has modifications to the input command for string inputs. The example below shows that the input command can receive strings by modifying the end of the command with ‘s’ after a comma after the standard input prompt. Several examples in the MATLAB script shown below compares numeric and string inputs.
>> example = input(‘Prompt typed here’, ‘s’)
The fprintf Command
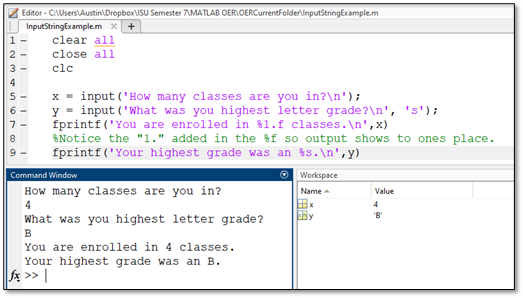
The disp and input functions enable the user to display information and input information into the code. However, these functions will be insufficient if the user wants to output information that changes based on inputs or other values in a script. As an example, let’s say a code was written to find the square of user input. The code may use a display function to inform the user of the code’s function and an input function to prompt the user to input a value. However, since the output changes depending on the input, a display value is unable to update to show this calculated output. The function fprintf is designed to display the value assigned to a variable inside of a text output message. The format for the fprintf is as follows:
>>fprintf ('Text text text %f text text text %f text text text %f \n',x,y,z)
Place a “%f” in each location where the value assigned to a variable should be displayed amongst a fixed message. The values of each variable input by the user are listed at the end of the function in a list separated by commas. Note that the included example is with three variables that happen to be named x, y, and z, respectively. fprintf follows the same format as the example when different numbers of variables are present.
The following example demonstrates input, and fprintf functions used together to provide the user instructions, allow the user to input data, and to output the processed data in a text message.
clc
clear
a=input('insert a: ');
b=input('insert b: ');
p=a*b;
n=a/b;
fprintf('%f multiplied by %f is %f \n and \n %f divided by %f is %f \n', a,b,p,a,b,n)
When using fprintf, the %f placeholder in the text output is specific to numeric variables. This means that it can only output numeric values. Alternative placeholders exist for different types of outputs that the user desires. The most common alternative to %f that may be encountered is %s, which outputs a string variable. String variables, as introduced previously, are letters or phrases assigned to a variable. Using %s allows users to output specific words within the defined output message. This is shown in the following example. Alternative placeholders can be viewed within the fprintf documentation on the MathWorks webpage that allows customization of everything from the decimal length in output to scientific notation to integer outputs.
Table 2.3.1
| Common Placeholder in fprintf | Usage |
| %f | Fixed point output (Most commonly used placeholder) |
| %s | Outputs a series of characters or a string |
| %i | Outputs an integer |
| %e or %E | Scientific notation with “e” displayed as a lowercase or uppercase, respectively |
| %g | Fixed point output (like %f) without trailing zeros. |
Modification of the %f operator can allow the user to control the precision of the output number. By default, the output number will include a large series of zeros at the end, which can be visually distracting and incorrect if that level of precision is not actually known.
Rounding
MATLAB has functions developed to round integers or array values within a code. The following functions are useful for rounding with standard rounding conventions, rounding to the floor, and rounding to the ceiling. These functions operate by modifying a variable and creating a new rounded variable. The following example shows how to round some variable a conventionally, to the floor, and to the ceiling and create a variable, b.
b = round(a)
b = floor(a)
b = ceiling(a)

![\sqrt[4]{(23-\frac{3}{2})} \sqrt[4]{(23-\frac{3}{2})}](https://rwu.pressbooks.pub/app/uploads/sites/46/2024/09/15d85f98c1057cb2ba38a8cfd7148b4c.png)
![\left[\frac{10\text{exp}(3/2)}{\sqrt{23}}\right] \left[\frac{10\text{exp}(3/2)}{\sqrt{23}}\right]](https://rwu.pressbooks.pub/app/uploads/sites/46/2024/09/9283312154d5096acc2c8213efc31bdd.png)
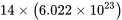
![\left[\frac{3^{3/2}-\sqrt3}{8+(\frac{4}{13})}\right]^3 \left[\frac{3^{3/2}-\sqrt3}{8+(\frac{4}{13})}\right]^3](https://rwu.pressbooks.pub/app/uploads/sites/46/2024/09/bb292a922130aeae5f8f703fe751befe.png)
