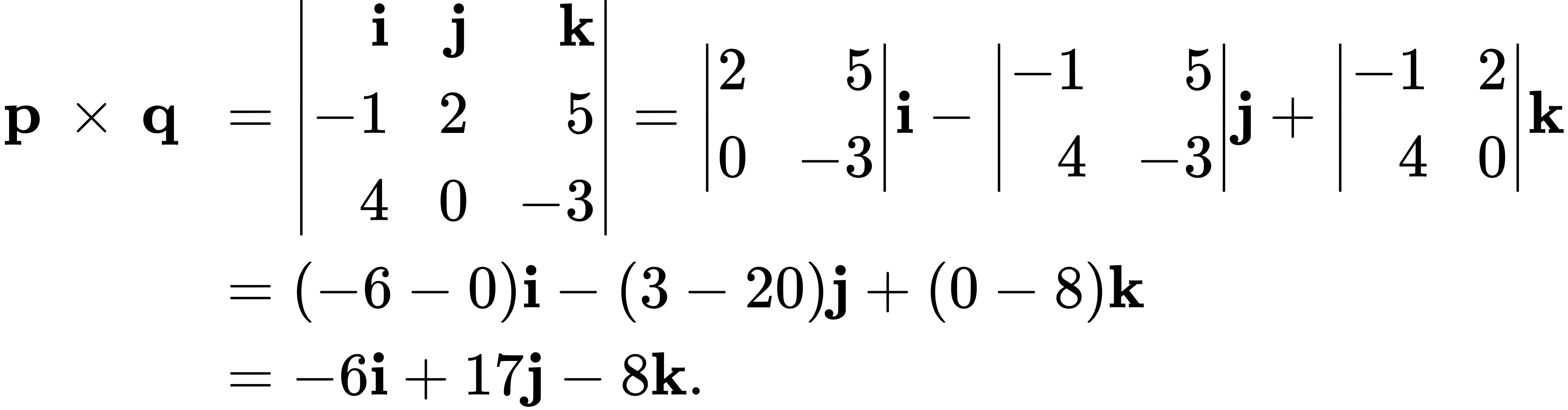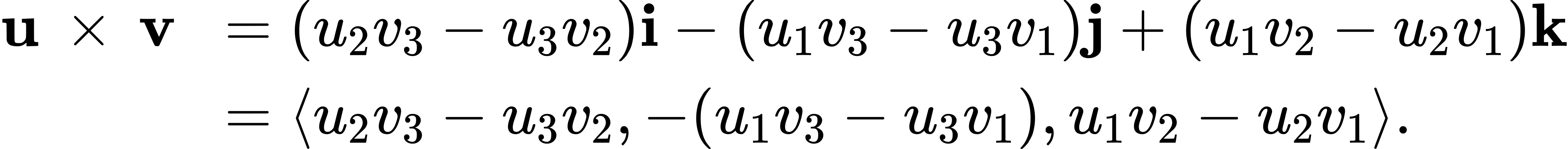4. The Cross Product
In this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to two given vectors.
The Cross Product and Its Properties
The dot product is a multiplication of two vectors that results in a scalar. In this section, we introduce a product of two vectors that generates a third vector orthogonal to the first two. Consider how we might find such a vector. Let u=![]() and v=
and v=![]() be nonzero vectors. We want to find a vector w=
be nonzero vectors. We want to find a vector w=![]() orthogonal to both u and v — that is, we want to find w such that u⋅w=0 and v⋅w=0. Therefore, w1, w2, and w3 must satisfy
orthogonal to both u and v — that is, we want to find w such that u⋅w=0 and v⋅w=0. Therefore, w1, w2, and w3 must satisfy
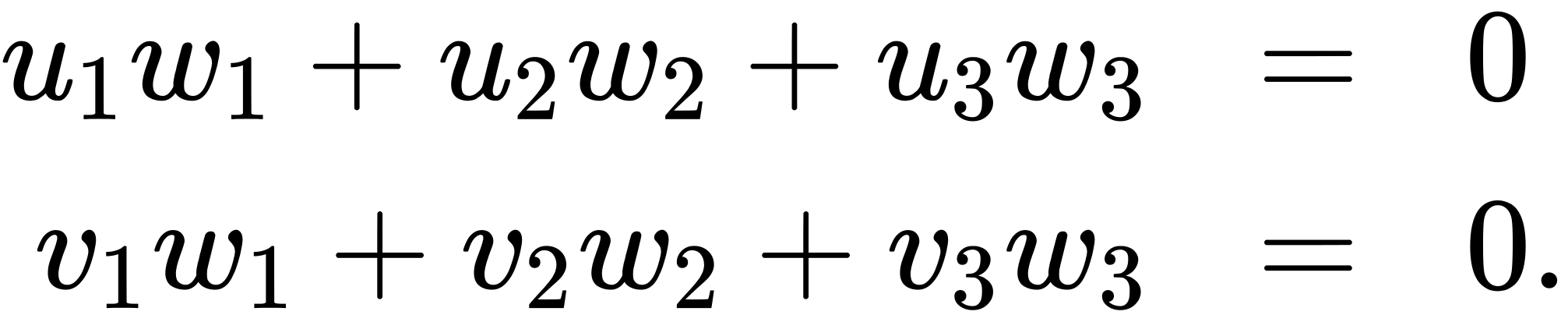
If we multiply the top equation by v3 and the bottom equation by u3 and subtract, we can eliminate the variable w3, which gives
(![]() −
−![]() )
) ![]() + (
+ (![]() −
−![]() )
) ![]() =0.
=0.
If we select
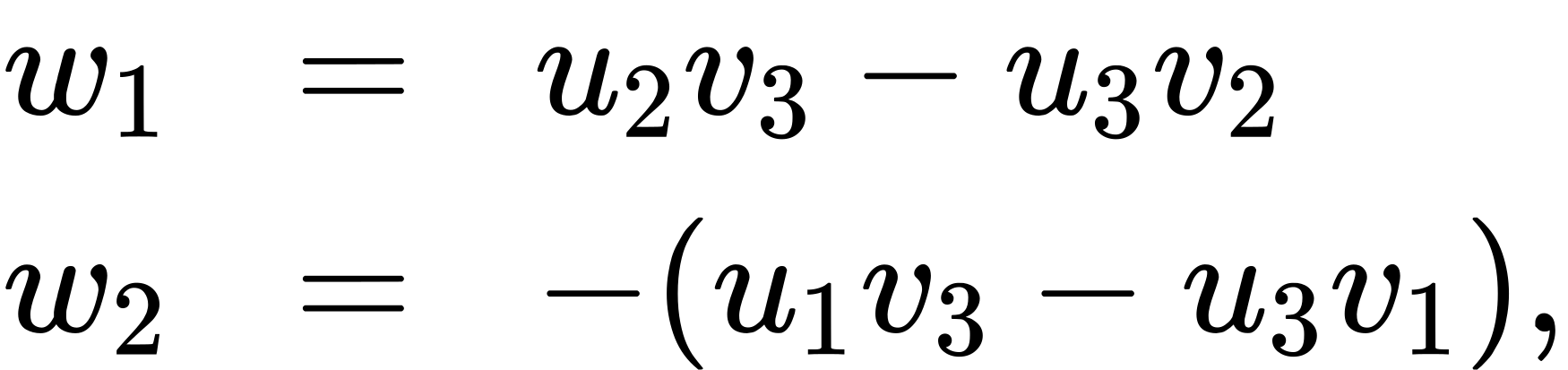
we get a possible solution vector. Substituting these values back into the original equations gives
![]() –
– ![]()
That is, vector
is orthogonal to both u and v, which leads us to define the following operation, called the cross product.
From the way we have developed u × v, it should be clear that the cross product is orthogonal to both u and v. However, it never hurts to check. To show that
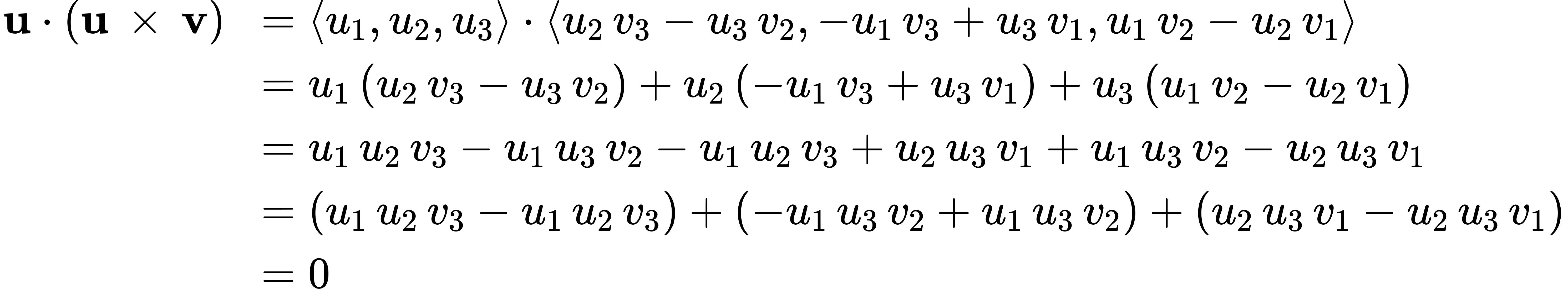
In a similar manner, we can show that the cross product is also orthogonal to v.
Example: Finding a Cross Product
Let p = ![]() and q =
and q = ![]() . Find p × q.
. Find p × q.
Solution
Substitute the components of the vectors into the definition of the cross product:
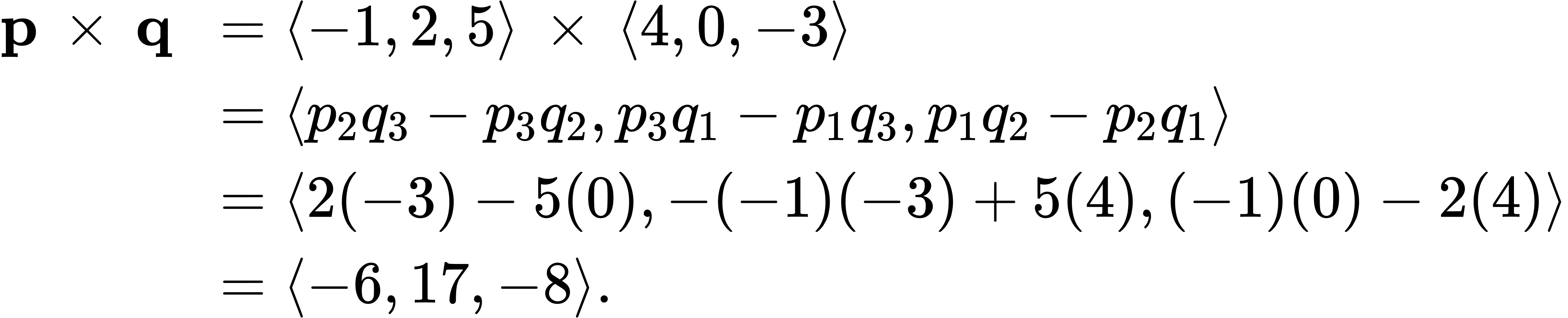
Although it may not be obvious from the definition of the cross product, the direction of u × v is given by the right-hand rule. If we hold the right hand out with the fingers pointing in the direction of u, then curl the fingers toward vector v, the thumb points in the direction of the cross product, as shown.
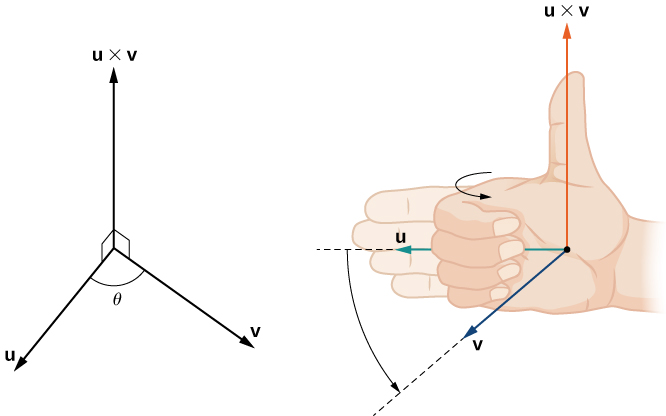
Notice what this means for the direction of v × u. If we apply the right-hand rule to v × u, we start with our fingers pointed in the direction of v, then curl our fingers toward the vector u. In this case, the thumb points in the opposite direction of u × v. (Try it!)
The cross products of the standard unit vectors i, j, and k can be useful for simplifying some calculations, so let’s consider these cross products. A straightforward application of the definition shows that
(The cross product of two vectors is a vector, so each of these products results in the zero vector, not the scalar 0.) It’s up to you to verify the calculations on your own.
Furthermore, because the cross product of two vectors is orthogonal to each of these vectors, we know that the cross product of i and j is parallel to k. Similarly, the vector product of i and k is parallel to j, and the vector product of j and k is parallel to i. We can use the right-hand rule to determine the direction of each product. Then we have
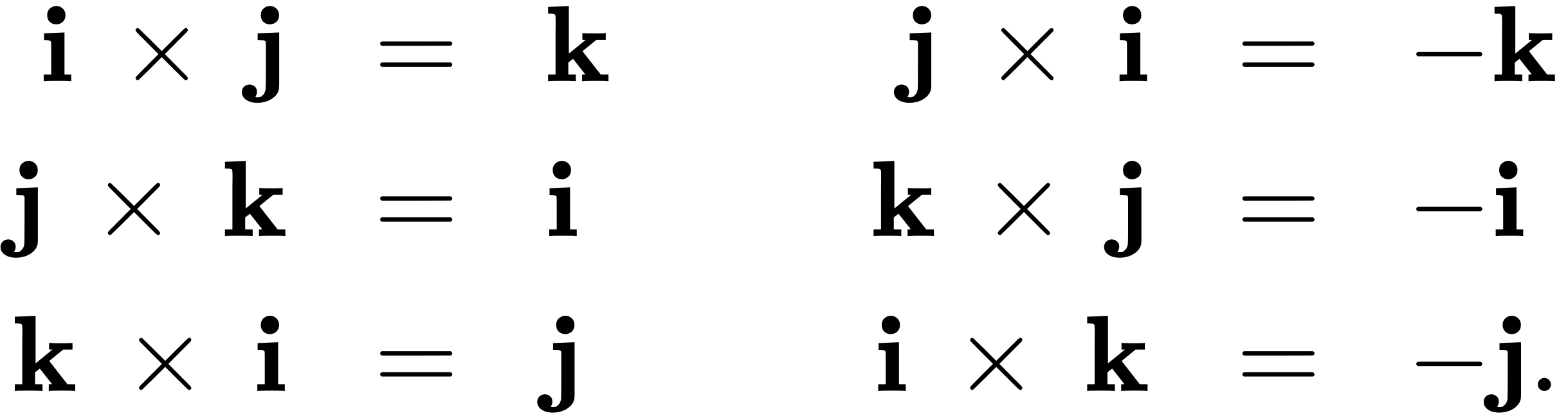
These formulas come in handy later.
Example: Cross Product of Standard Unit Vectors
Find i × ( j × k ).
Solution
We know that j × k = i. Therefore, i × (j × k) = i × i=0.
As we have seen, the dot product is often called the scalar product because it results in a scalar. The cross product results in a vector, so it is sometimes called the vector product. These operations are both versions of vector multiplication, but they have very different properties and applications. Let’s explore some properties of the cross product. We prove only a few of them. Proofs of the other properties are left as exercises.
Theorem
Properties of the Cross Product
Let u, v, and w be vectors in space, and let c be a scalar.
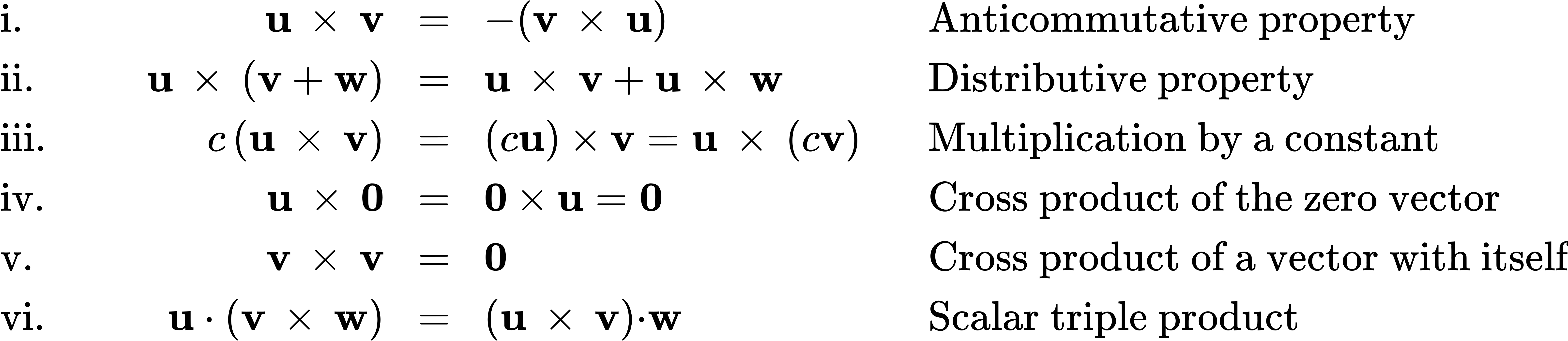
Proof
For property i., we want to show u × v = -(v × u). We have
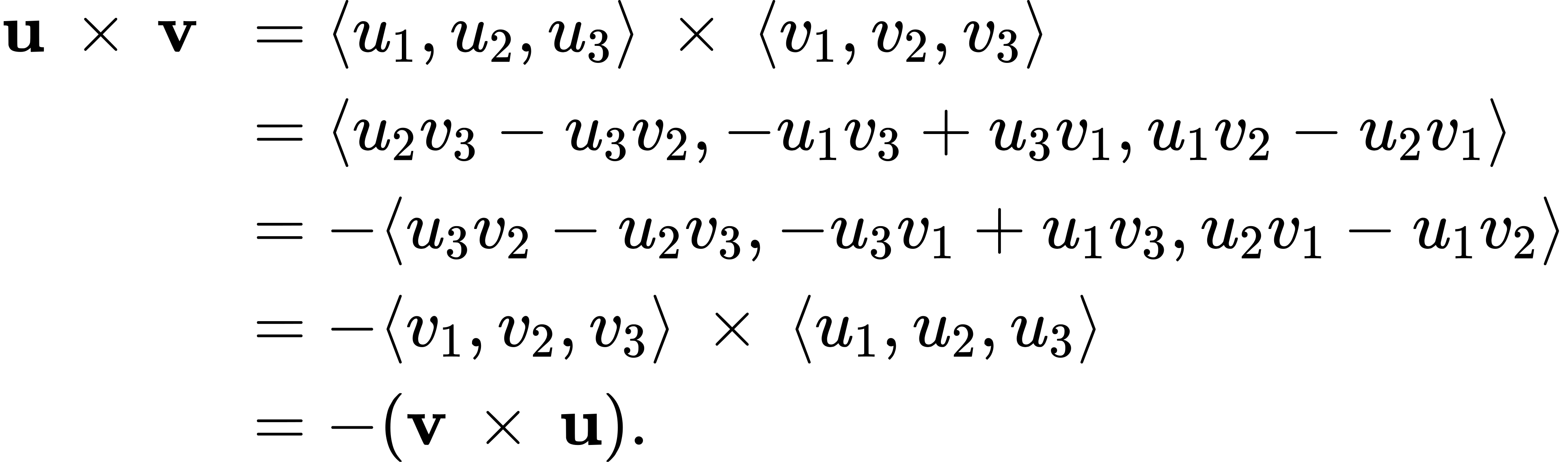
Unlike most operations we’ve seen, the cross product is not commutative. This makes sense if we think about the right-hand rule.
For property iv., this follows directly from the definition of the cross product. We have
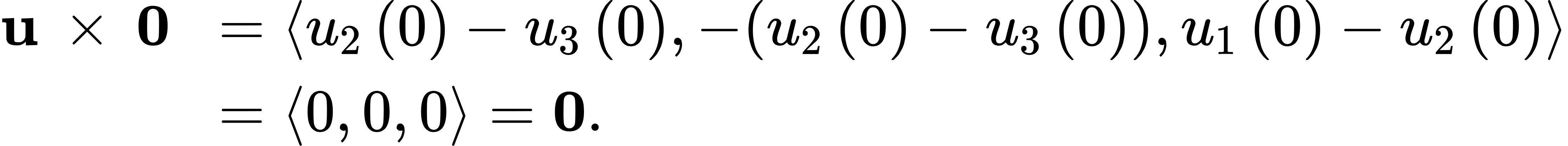
Then, by property i., 0 × u=0 as well. Remember that the dot product of a vector and the zero vector is the scalar 0, whereas the cross product of a vector with the zero vector is the vector 0.
Property vi. looks like the associative property, but note the change in operations:
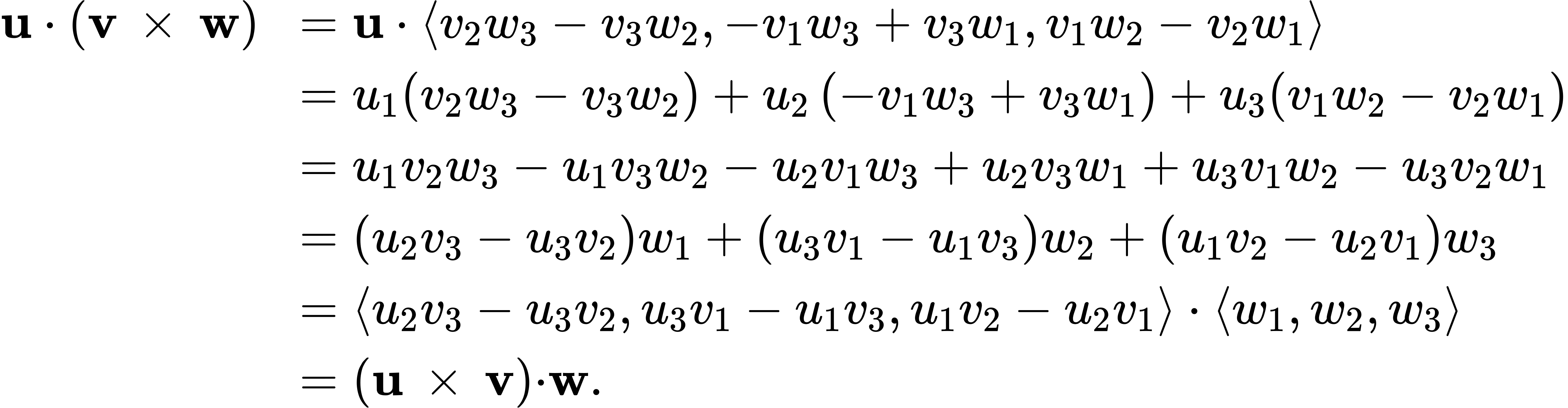
□
So far in this section, we have been concerned with the direction of the vector u × v, but we have not discussed its magnitude. It turns out there is a simple expression for the magnitude of u × v involving the magnitudes of u and v, and the sine of the angle between them.
Theorem
Magnitude of the Cross Product
Let u and v be vectors, and let θ be the angle between them.
Then, || u × v ||=||u||⋅||v||⋅sin θ.
Proof
Let u=![]() and v=
and v=![]() be vectors, and let θ denote the angle between them. Then
be vectors, and let θ denote the angle between them. Then
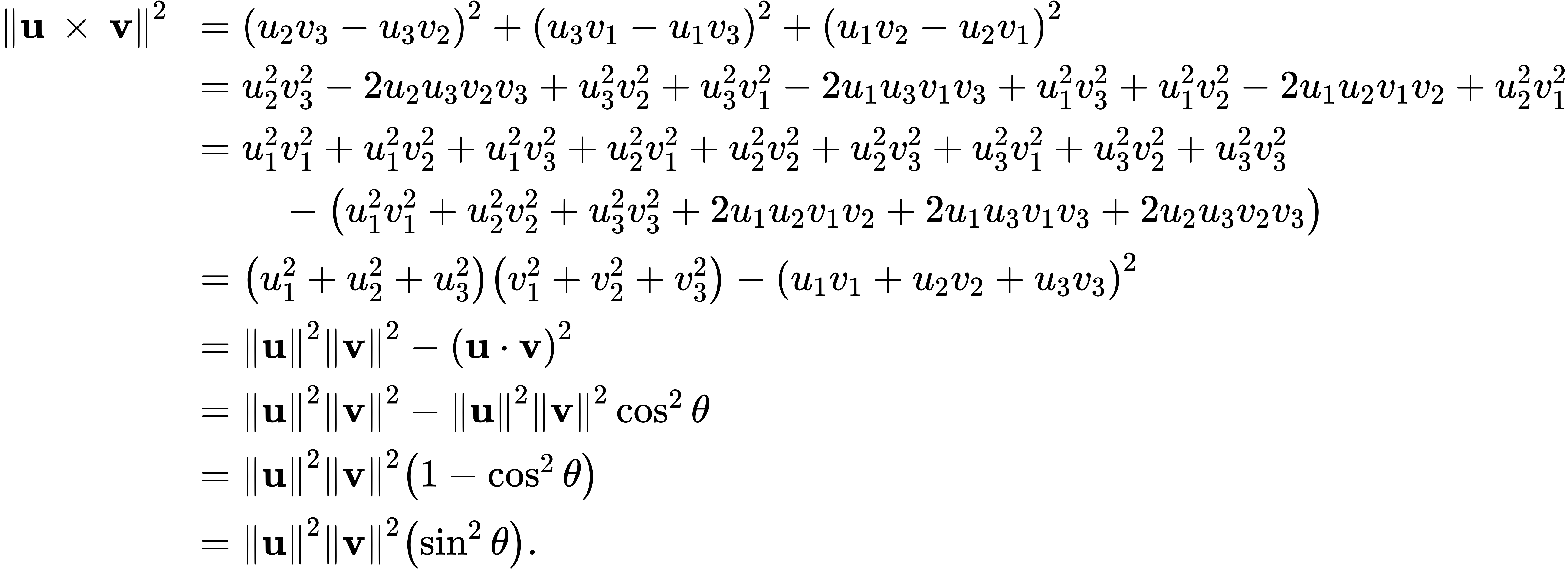
Taking square roots, we have the desired result:
||u × v||=||u|| ||v|| sin θ.
□
This definition of the cross product allows us to visualize or interpret the product geometrically. It is clear, for example, that the cross product is defined only for vectors in three dimensions, not for vectors in two dimensions. In two dimensions, it is impossible to generate a vector simultaneously orthogonal to two nonparallel vectors.
Example: Calculating the Cross Product
Use the Properties of the Cross Product to find the magnitude of the cross product of
u = ![]() and v =
and v = ![]()
Solution
We have
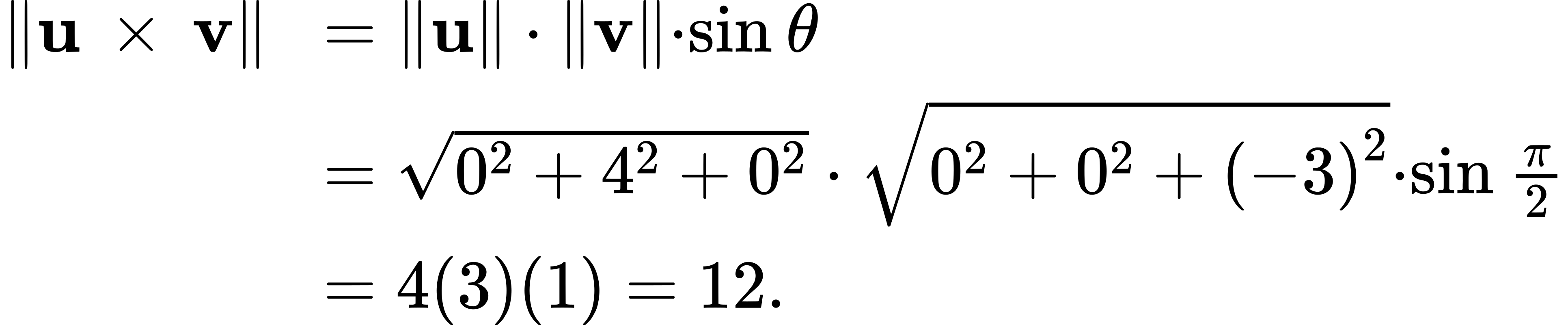
Determinants and the Cross Product
Using the definition of the cross product to find the cross product of two vectors is straightforward, and it presents the cross product in the useful component form. The formula, however, is complicated and difficult to remember. Fortunately, we have an alternative. We can calculate the cross product of two vectors using determinant notation.
A 2 × 2 determinant is defined by
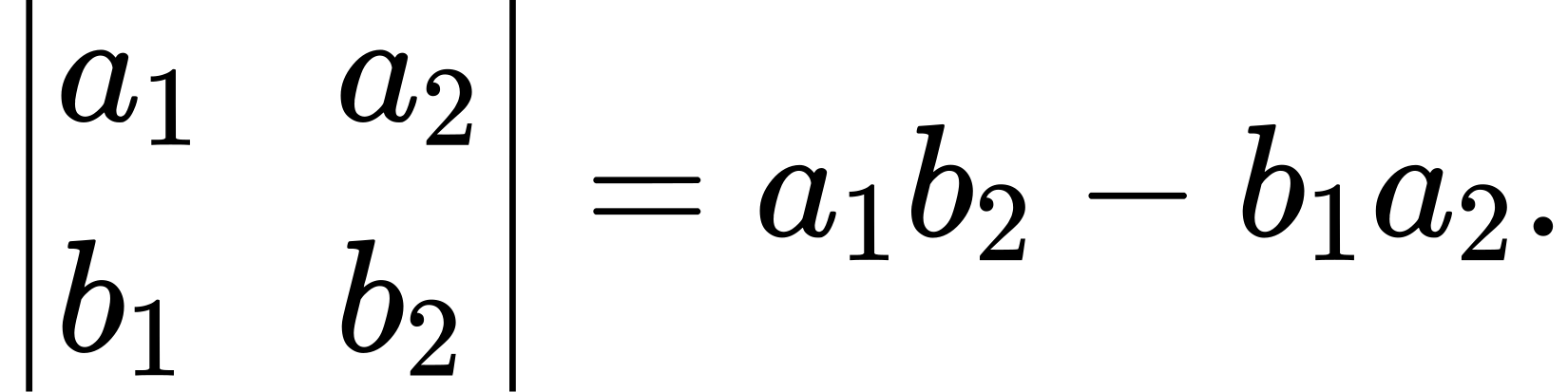
For example,
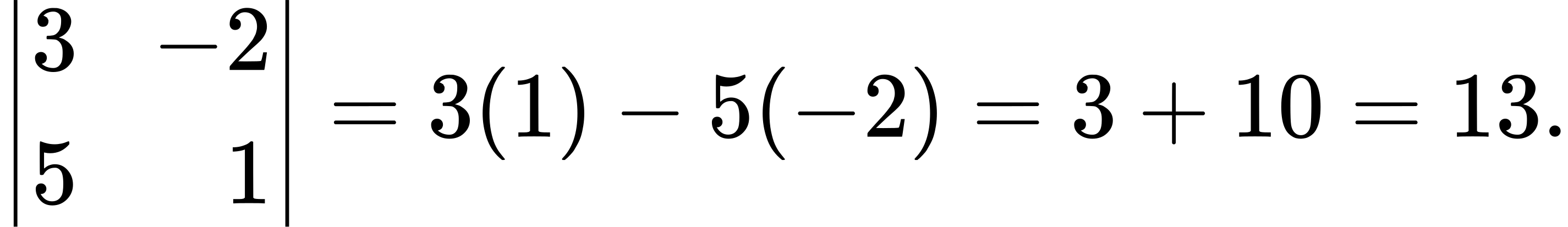
A 3 × 3 determinant is defined in terms of 2 × 2 determinants as follows:
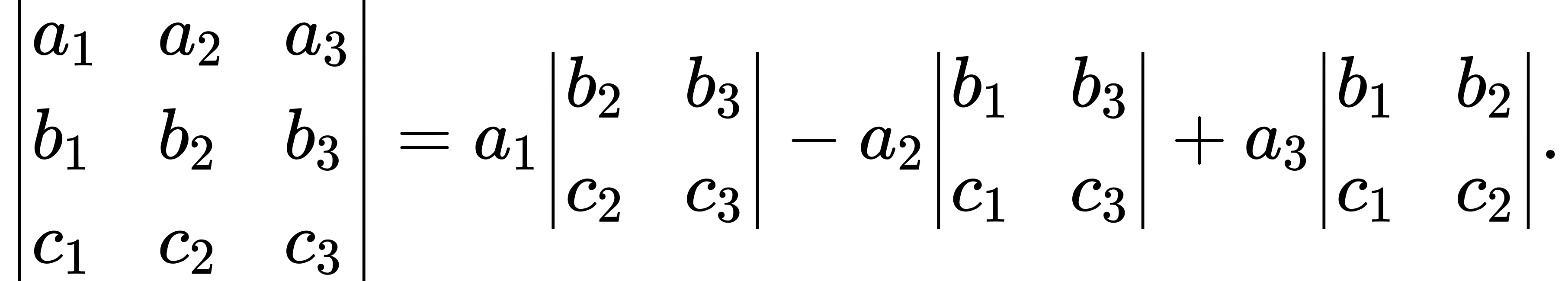
The equation above is referred to as the expansion of the determinant along the first row. Notice that the multipliers of each of the 2 × 2 determinants on the right side of this expression are the entries in the first row of the 3 × 3 determinant. Furthermore, each of the 2 × 2 determinants contains the entries from the 3 × 3 determinant that would remain if you crossed out the row and column containing the multiplier. Thus, for the first term on the right, a1 is the multiplier, and the 2 × 2 determinant contains the entries that remain if you cross out the first row and first column of the 3 × 3 determinant. Similarly, for the second term, the multiplier is a2, and the 2 × 2 determinant contains the entries that remain if you cross out the first row and second column of the 3 × 3 determinant. Notice, however, that the coefficient of the second term is negative. The third term can be calculated in similar fashion.
Example: Using Expansion Along the First Row to Compute a 3 × 3 Determinant
Evaluate the determinant
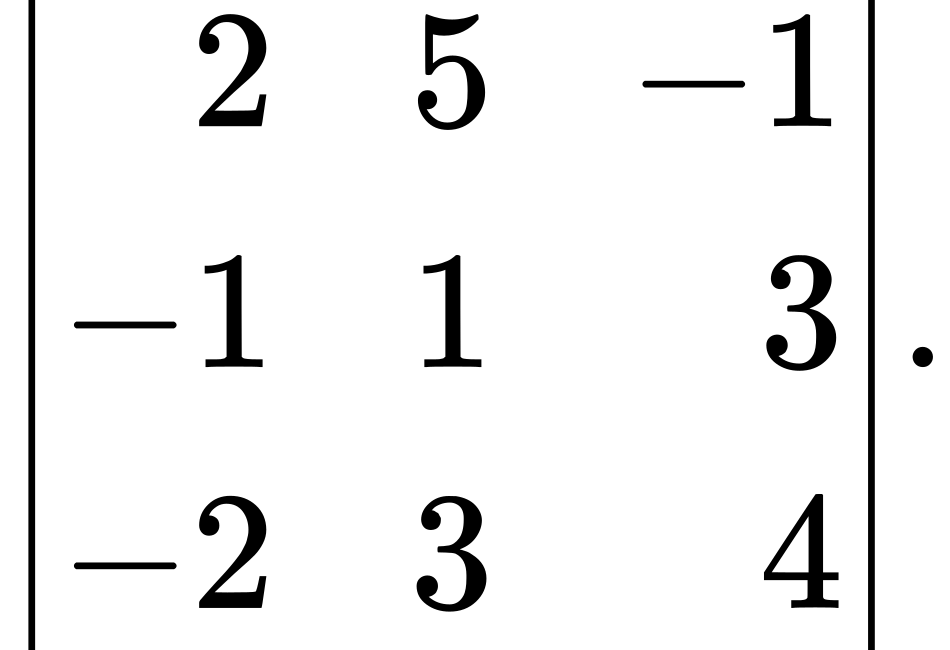
Solution
We have
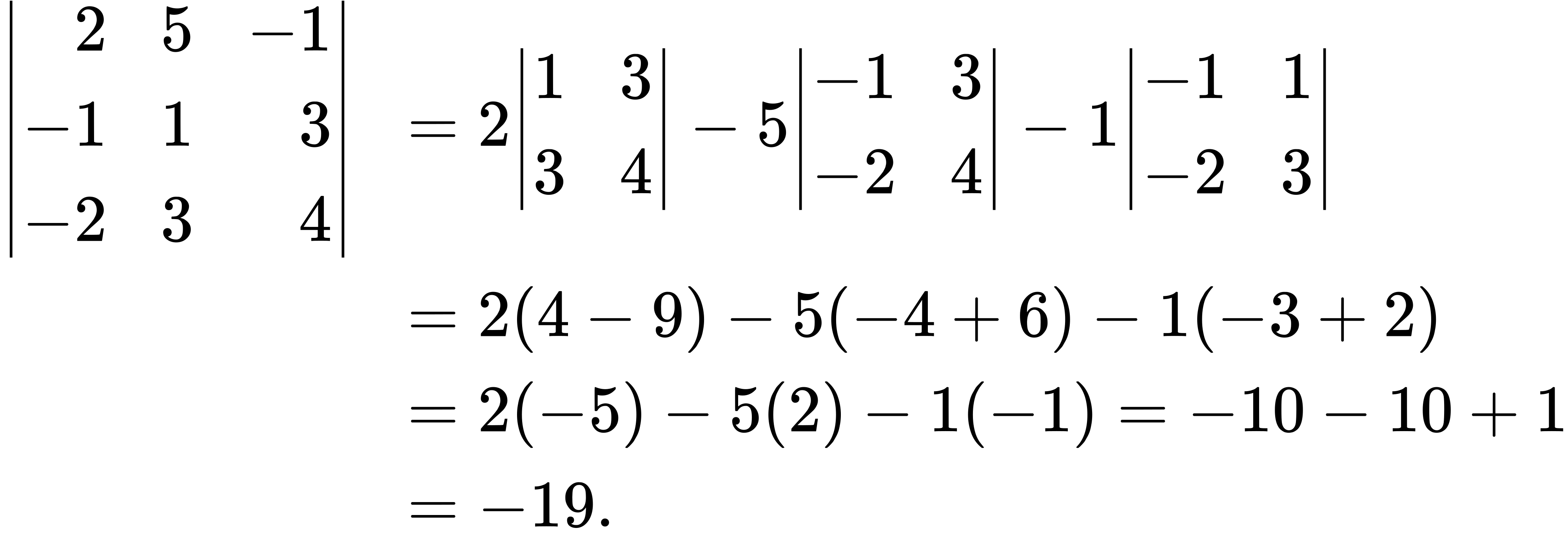
Technically, determinants are defined only in terms of arrays of real numbers. However, the determinant notation provides a useful mnemonic device for the cross product formula.
Rule: Cross Product Calculated by a Determinant
Let u=![]() and v=
and v=![]() be vectors. Then the cross product u × v is given by
be vectors. Then the cross product u × v is given by
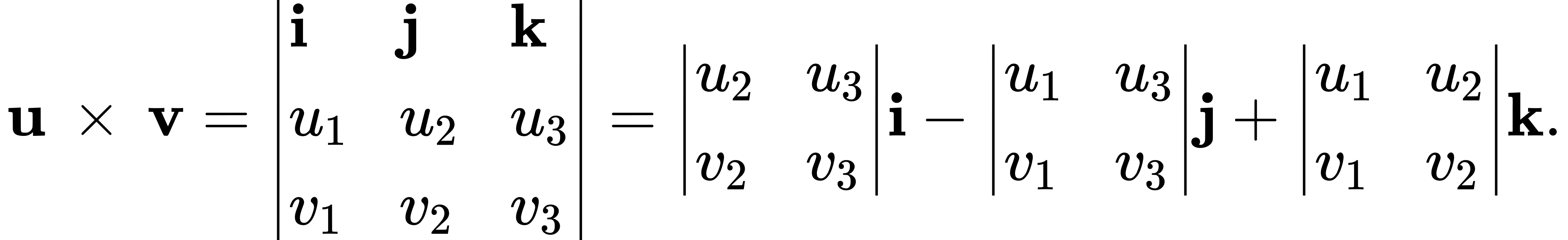
Example: Using Determinant Notation to find p × q
Let p=![]() and q=
and q=![]() . Find p × q.
. Find p × q.
Solution
We set up our determinant by putting the standard unit vectors across the first row, the components of u in the second row, and the components of v in the third row. Then, we have