The Harmonic Series and the Perfect Fifth

Drawing from foundational studies in musicianship and music fundamentals, one realizes the profound significance of the harmonic series in the realm of music. Not only is it pivotal in shaping our perception of tone color (timbre), but it also lays the groundwork for understanding harmonic structures like chords and the nature of tonality. Broadly speaking, as one progresses up the harmonic series from a given fundamental, the tonal relationship with the fundamental becomes more distant. Moreover, the frequency with which a tone recurs within the series can be viewed as an indicator of its relationship or kinship with the fundamental — the most recurrent tone in the series.

To illustrate, in Figure 1 where C serves as the fundamental, the first thirteen overtones reveal C four times, more than any other tone in this overtone set (up to the 14th harmonic). Following C, G makes its appearance thrice, and subsequently, E is seen twice, and the pattern continues. From this observation, one can infer that G holds the most harmonious relationship to C, the fundamental, with E trailing closely behind.
Given that G shares the closest tonal affinity with C, and the interval between C and G is a perfect fifth, it stands to reason that the perfect fifth emerges as the most stable interval, second only to the octave. This interval encapsulates a pivotal relationship within the harmonic series. Observing the fifth relationships starting from C, as depicted in Figure 1, we find a sequence: C-G-D-A, with E up next. This interval, accompanied by the array of tones more distantly related to the fundamental, underpins our comprehension of expansive harmonic relationships in tonal music.

Tonal Scale Degree Functions

Major Mode

Before delving further, let’s briefly review the scale degrees in the major mode and their associated names:

Scale Degree Functions (Major): Names and Abbreviations

ABBREVIATION	NAME
T	TONIC
ST	SUPERTONIC
M	MEDIANT
SD	SUBDOMINANT
D	DOMINANT
SM	SUBMEDIANT
LT	LEADING-TONE

Minor Mode

Scale Degree Functions (MINOR): Names and Abbreviations

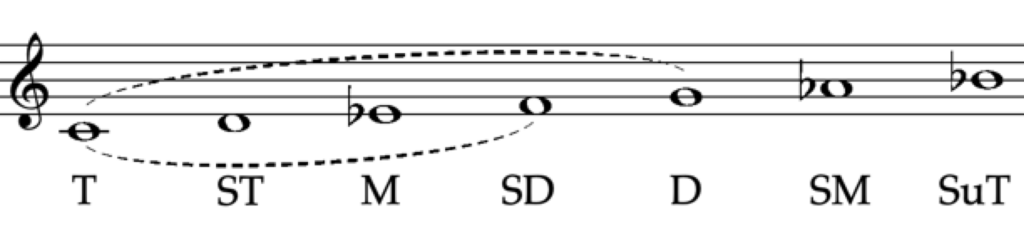
ABBREVIATION	NAME
T	TONIC
ST	SUPERTONIC
M	MEDIANT
SD	SUBDOMINANT
D	DOMINANT
SM	SUBMEDIANT
SuT	SUBTONIC

Scale Degree Relationships and Definitions

Now that we have reacquainted ourselves with the names of each scale degree in both major and minor scales, let’s briefly explore the reasons behind these names.

TONIC

The term “tonic” describes the tone around which music revolves, often referred to as “home”. In diatonic tonal and modal music, this tone is known as the modal/tonal center. All other scale degrees are labeled relative to this tone, with relationships defined by intervals and distance from the tonal center. Notably, the position of the tonal center in diatonic tonal/modal music indicates the locations of the two half-steps and the tritone. These relationships define each mode and grant each mode its unique sound characteristics. We touched upon this concept earlier when studying modal counterpoint:

• In the major mode (Ionian), the two half-steps are between scale degrees 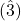and 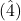and between and 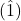. The tritone is between 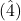and .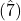
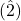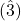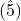• In the natural minor mode (Aeolian), the two half-steps are between and and and 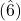, with the tritone between 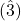and .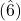

DOMINANT and SUBDOMINANT

The Dominant is the tone located a perfect fifth above a given fundamental tone. Owing to the harmonic series, the Dominant is intrinsically linked to the fundamental tone. In tonal and modal music, the tone that is a perfect fifth above the tonic is labeled the Dominant, and corresponds to scale degree .

The Subdominant is the tone located a perfect fifth below the fundamental tone. This relationship mirrors that of the Tonic and Dominant; if you consider the Tonic as the Dominant of the Subdominant. The term “sub” signifies “below”, prompting us to think of the Subdominant as a “lower Dominant”. The tone a perfect fifth below the Tonic (or a perfect fourth above, by inversion) corresponds to scale degree .

MEDIANT and SUBMEDIANT

The Mediant, situated on scale degree , earns its name as it mediates the distance between the Tonic and the Dominant. This tone seamlessly blends with the Tonic due to its position in the harmonic series.

The Submediant, on scale degree , acts similarly, mediating the distance between the Tonic and the Subdominant. It’s the tone second in relation to the Subdominant within the harmonic series.

Moreover, the Mediant and Submediant are linked by a perfect fifth: the Mediant is the Submediant’s Dominant, and vice versa. The term “sub” means “below”, suggesting the Submediant is a “lower Mediant”.

SUPERTONIC and SUBTONIC (minor)

The Supertonic is the tone one whole step above the Tonic, found on scale degree . The term “super” translates to “above”. The Supertonic is a perfect fifth above the Dominant, making it the Dominant’s Dominant and thereby its most related tone in the harmonic series. In major scales, the Supertonic also maintains a perfect fifth relationship with the Submediant.

Conversely, the Subtonic, found in natural minor scales, is one whole step below the Tonic, matching scale degree . The term “sub”, as defined earlier, means “below”. The Subtonic and Subdominant share a perfect fifth relationship, making the Subtonic the Subdominant’s Subdominant. This places the Subdominant as the closest tone to the Subtonic by means of the harmonic series.

LEADING-TONE

The Leading-Tone is named for its tendency to “lead” to the Tonic. By definition, it’s a half-step below the Tonic. This half-step has a strong melodic pull when ascending, an important characteristic in the mode. Additionally, it’s integral to the harmonic resolution of the tritone, a topic we’ll delve deeper into in the next chapter. While naturally occurring in major scales, it must be raised by a half-step in minor scales, a modification found in both harmonic and melodic minor scales.

Tonal Scale Degree Functions

The Major Mode Perfect Fifth Pair Relationships

Each scale degree, barring two exceptions, has an upper and lower perfect fifth interval relationship. These are defined by the harmonic series and are associated with two other scale degrees. Another perspective on these relationships views them as sets of relative Dominants and SubDominants for each scale degree. The Dominant is defined as a tone a perfect fifth above a given fundamental note, while the SubDominant lies a perfect fifth below. We can explore each of these relationships in the major mode in detail.

Tonic-Dominant Pair & Dominant-SuperTonic Pair

The foremost and most pivotal of these perfect fifth “polarities” is established on the Tonic scale degree . A crucial concept to understand is the inherent desire of the Dominant tone, located a fifth above, to resolve to or merge with the Tonic. This inclination is rooted in the harmonic series. Likewise, the Tonic gravitates towards the SubDominant, situated a perfect fifth below. Figure 3 illustrates this in the key of C major, with the flow of tones moving downward by perfect fifths, denoted by red arrows. The term “SubDominant” translates to “lower Dominant.” As such, the SubDominant continuously draws the Tonic towards it, making it the most potent tone in the mode due to the natural laws of the harmonic series. This dynamic tension—between the Dominant’s pull to the Tonic and the Tonic’s attraction to the SubDominant—creates the fundamental ebb and flow in tonal music’s harmonic progressions.

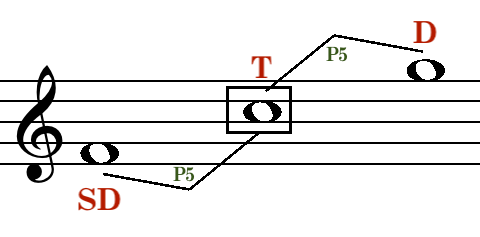
Expanding on this, the second most vital polarity in the mode involves the Dominant. When viewed locally, the Dominant, while sounding, takes on the role of a secondary Tonic. It naturally has its upper perfect fifth counterpart, the SuperTonic, wanting to bond with it. Similarly, as previously discussed, it wishes to move to and merge with the Tonic.

SuperTonic-SubMediant Pair & SubMediant-Mediant Pair

Moving on, if we treat the SuperTonic as a localized tonic when sounded, it possesses an upper Dominant, the SubMediant, that seeks to resolve to it. Following this logic, the Dominant functions as the lower fifth SubDominant.

SubDominant-Mediant Pair

Concluding, we examine the relationships around the SubDominant and the Mediant. In the SubDominant’s case, we recognize the already familiar upper relative Dominant as the Tonic, which tends to descend to the SubDominant. However, the major mode’s SubDominant does not possess a lower SubDominant perfect fifth. Therefore, within any major key, the SubDominant acts as a kind of boundary, preventing forward movement without modulating (changing the key or mode). Likewise, for the Mediant, a stable relative Dominant does not exist since the Leading-Tone lacks a consistent fifth as part of its harmony, being either the diminished triad or diminished seventh chord.

The Minor Mode Perfect Fifth Pair Relationships

Similar to the major mode, we can explore the relationships in the upper and lower perfect fifth polarities in the minor mode. Notably, some variations exist due to the two different forms of minor, which cause slight alterations in the relationships. The quality of the chords—whether major or minor (excluding any unstable diminished chords)—is secondary. The primary focus is on the interval relationships between scale degrees. For instance, the function of the Dominant in the minor mode remains consistent, even though the quality of the chords built on the Dominant can shift from minor to major depending on the form of minor (Natural-Descending or Ascending). Let’s examine some specifics:

Tonic-Dominant Pair & Dominant-SuperTonic Pair

The Tonic polarity (from Tonic up to Dominant and down to SubDominant) is consistent with the major mode. However, in the natural form of minor, the Dominant polarity varies as the SuperTonic lacks stable harmony due to the diminished chord typically built on it. This changes in the ascending form of the minor (Melodic), where a stable SuperTonic minor triad emerges:

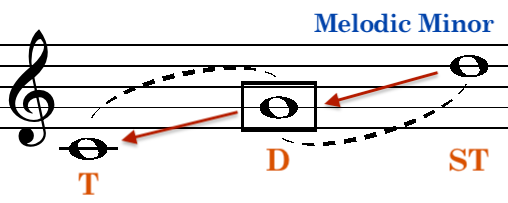
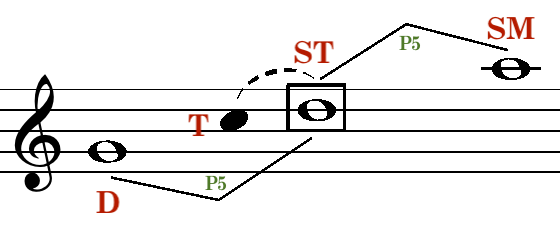
SubDominant-Tonic Pair & SubTonic-SubDominant Pair

In natural minor, a stable SubTonic introduces a new polarity: SubDominant-Tonic. Here, the SubDominant feels a gravitational pull downwards to the SubTonic. Additionally, the SubTonic-SubDominant polarity arises, where the SubTonic is drawn towards the SubMediant.

Mediant-SubTonic Pair & SubMediant-Mediant Pair

The Mediant-SubTonic polarity emerges, where the Mediant feels drawn to the SubMediant. With the SubMediant-Mediant polarity, the lack of a stable SuperTonic prevents a downward pull from the SubMediant. One might wonder if, in the ascending form, the raised SuperTonic creates a stable relationship with the SubMediant. It is a good question; however, despite the presence of a stable SuperTonic in the ascending form of the minor, the SubMediant does not establish a strong gravitational pull towards it. The raised 6th and 7th scale degrees introduce a different melodic and harmonic context, altering our perception of the inherent relationships.

Harmonic Function in Tonality

Having revisited the scale degrees in major and minor modes and examined the profound influence of the perfect fifth relationships among these degrees, we can broaden our view to encompass the concept of tonal harmonic function. In essence, there are three tonal regions:

• Tonic Region: Stable and at rest, it reinforces the key/tonal center.
• SubDominant Region: Restless and in contrast with the key/tonal center, it evokes a sense of movement.
• Dominant Region: The most unstable region, it exhibits a compelling pull towards the Tonic region, playing a crucial role in maintaining the balance of the key/tonal center.

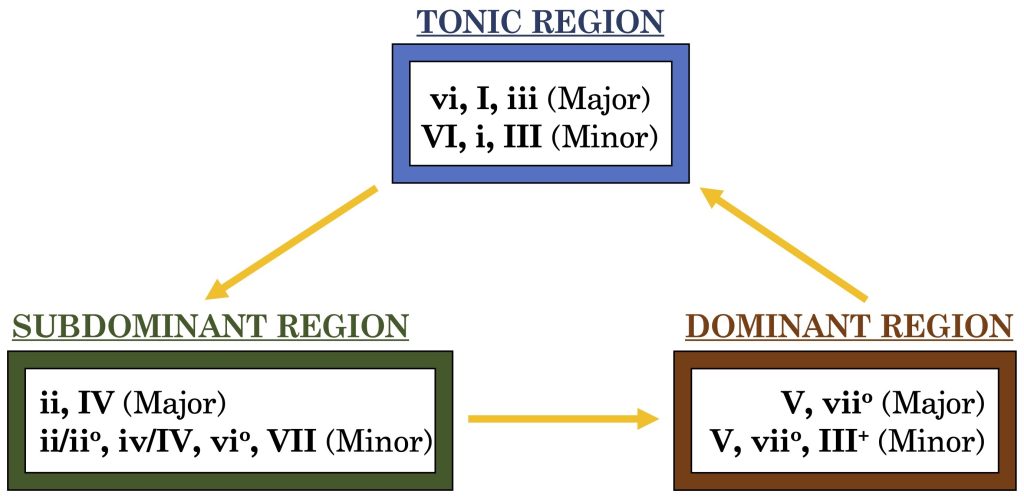
Above (Fig. 20) is a flowchart that delineates each of the three tonal regions. The yellow arrows indicate the harmony’s propensity to transition between these regions. Notably, the chart’s counter-clockwise orientation mirrors its representation on the Circle of Fifths, underscoring the progression in descending fifths through the scale degrees.

When mapped directly to a Circle of Fifths in each mode, we can see the counterclockwise flow of tonal gravity directly.

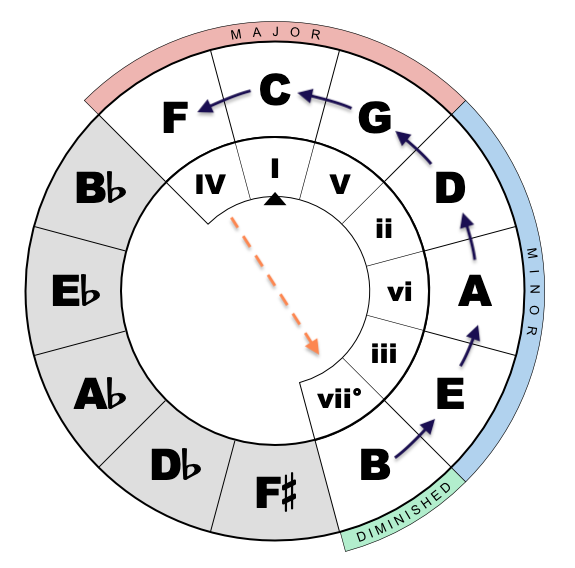
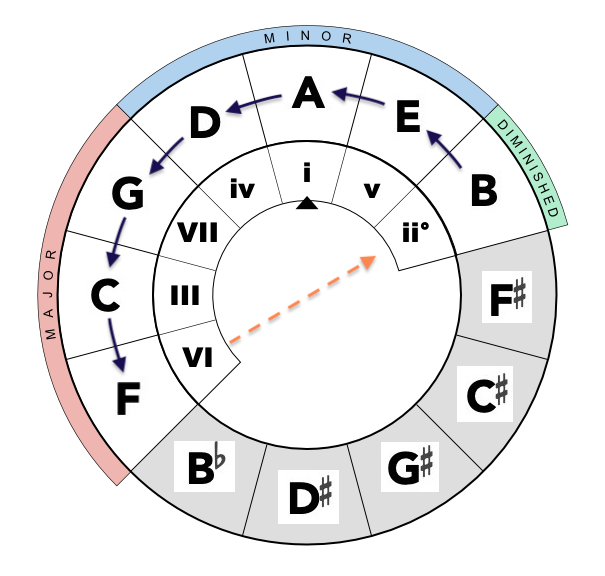
It’s important to recognize that at a certain juncture across the circle, the pattern of fifths doesn’t maintain a stable perfect fifth, depicted by the dashed yellow line. In fact, the tonal pull in the mode effectively ends at this point, and we must “push” back against this natural tendency unless we move to another key/mode.

We may summarize the above in two main points:

1. The harmonic series substantiates the perfect fifth and the downward pull from Dominant to Tonic, alongside the analogous pulls of the secondary scale degrees.
2. The progression is cyclical: The Tonic leads to the SubDominant, which subsequently gravitates towards the Dominant, eventually returning to the Tonic.

Harmonic Progression: The Root Motion

Before moving forward into the application of scale degree functions and tonal functions, we need to delve into another facet of harmony: the root motion between chords. Until now, our primary focus has been on voice-leading and the seamless connection of voices through common tones. But how do we measure the relative strength of a chord transition? This is determined by observing how the roots of each chord relate to one another. Essentially, there are three main types of harmonic motion: Strong, Weak, and Adjacent.

Strong Harmonic Motion

A strong motion is characterized by its ability to impart a sense of forward momentum in a musical phrase. More specifically, it refers to a chord transition in which the next chord’s root is introduced as a new element. Put another way, the new tone that emerges becomes the root of the subsequent chord. There are two primary root motions that usher in the root as a fresh chord tone:

• UPWARD by a Fourth
• DOWNWARD by a Third

Weak Harmonic Motion

Conversely, weak motion doesn’t offer a sense of progression. Instead, it creates a feeling of stasis, even when there are changes in the musical texture. In technical terms, it pertains to a chord transition where the subsequent chord’s root is already present in the preceding chord, meaning the next root serves as a shared tone between the two chords. Two prevalent root motions retain the root as a shared tone:

• UPWARD by a Third
• DOWNWARD by a Fourth

Adjacent Root Motion

Finally, we have the adjacent root motion where all chord tones undergo a change. Depending on the context, this motion can be categorized as either “strong” or “weak”. It’s worth noting that overusing this motion can potentially disrupt the fluent harmonic progression of a musical phrase, so it should be employed judiciously.

Aesthetic Considerations of Root Motion

When used judiciously, all three types of harmonic motion contribute to the musical ebb and flow in tonality. It’s crucial to understand that the labels “strong” and “weak” are not value judgments. A “strong” motion isn’t inherently superior, just as a “weak” motion isn’t inherently inferior. At times, a “weak” motion might be preferred within a chord progression to sustain interest, provide a restful moment, or introduce embellishments. Ultimately, achieving a balance is paramount to ensure diversity and alignment with the overarching musical objective.