POSTLUDE: Fundamentals of Music (Review – From “Open Music Theory”)
30 Major Scales, Scale Degrees, and Key Signatures
Chelsey Hamm and Bryn Hughes
Key Takeaways
- A major scale is an ordered collection of half and whole steps with the ascending succession W‑W‑H‑W‑W‑W‑H.
- Major scales are named for their first note (which is also their last note), including any accidental that applies to the note.
- Scale degrees are solmization syllables notated by Arabic numerals with carets above them. The scale degrees are
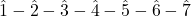 .
. - Solfège solmization syllables are another method of naming notes in a major scale. The syllables are do, re, mi, fa, sol, la, and ti.
- Each note of a major scale is also named with scale-degree names: tonic, supertonic, mediant, subdominant, dominant, submediant, and leading tone.
- A key signature, consisting of either sharps or flats, appears at the beginning of a composition, after a clef but before a time signature.
- The order of sharps in key signatures is F, C, G, D, A, E, B, while the order of flats is the opposite: B, E, A, D, G, C, F. In sharp key signatures, the last sharp is a half step below the tonic (the first note of a scale). In flat key signatures, the second-to-last flat is the tonic.
- The circle of fifths is a convenient visual for remembering major key signatures. All of the major key signatures are placed on a circle in order of number of accidentals.
A scale is an ordered collection of half and whole steps (see Half and Whole Steps and Accidentals to review).
Major Scales
A major scale is an ordered collection of half- (abbreviated H) and whole steps (abbreviated W) in the following ascending succession: W-W-H-W-W-W-H. Listen to Example 1 to hear an ascending major scale. Each whole step is labeled with a square bracket and “W,” and each half step is labeled with an angled bracket and “H.”
https://musescore.com/user/32728834/scores/6815731/embed
Example 1. An ascending major scale.
A major scale always starts and ends on notes of the same letter name, one octave apart, and this starting and ending note determines the name of the scale. Therefore, Example 1 depicts a C major scale because its first and last note is a C.
The name of a scale includes any accidental that applies to the first and last note. Example 2 shows a B♭ (B-flat) major scale—not a B major scale, which would use a different collection of pitches. Note that the pattern of half and whole steps is the same in every major scale, as shown in Example 1 and Example 2.
https://musescore.com/user/32728834/scores/6823280/embed
Example 2. A B-flat major scale.
Scale Degrees, Solfège, and Scale-Degree Names
Musicians name the notes of major scales in several different ways. Scale degrees are solmization syllables notated by Arabic numerals with carets above them. The first note of a scale is ![]() and the numbers ascend until the last note of a scale, which is also
and the numbers ascend until the last note of a scale, which is also ![]() (although some instructors prefer
(although some instructors prefer ![]() ). Example 3 shows a D major scale with each scale degree labeled with an Arabic numeral and a caret.
). Example 3 shows a D major scale with each scale degree labeled with an Arabic numeral and a caret.
https://musescore.com/user/32728834/scores/8452298/embed
Example 3. A D major scale.
Below the scale degrees, Example 3 also shows another method of naming notes in a major scale: solfège solmization syllables. Solfège (a system of solmization syllables) are another method of naming notes in a major scale. The syllables do, re, mi, fa, sol, la, and ti can be applied to the first seven notes of any major scale; these are analogous to the scale degrees ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The last note is do (
. The last note is do (![]() ) because it is a repetition of the first note. Because do (
) because it is a repetition of the first note. Because do (![]() ) changes depending on what the first note of a major scale is, this method of solfège is called movable do. This is in contrast to a fixed do solmization system, in which do (
) changes depending on what the first note of a major scale is, this method of solfège is called movable do. This is in contrast to a fixed do solmization system, in which do (![]() ) is always the pitch class C.
) is always the pitch class C.
Each note of a major scale is also named with scale-degree names: tonic, supertonic, mediant, subdominant, dominant, submediant, leading tone, and then tonic again. Example 4 shows how these names align with the scale-degree number and solfège systems described above.
[table “37” not found /]
Example 4. Scale-degree numbers, solfège syllables, and scale-degree names.
Example 5 shows these scale-degree names applied to an A♭ major scale:
https://musescore.com/user/32728834/scores/8452340/embed
Example 5. An A♭ major scale with scale-degree names.
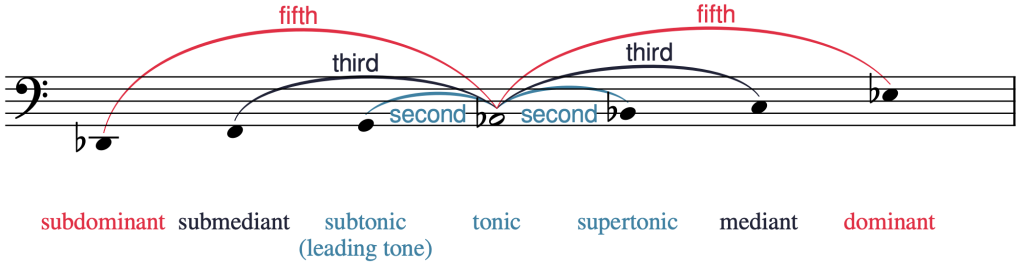
Example 6 shows the notes and scale-degree names of the A♭ major scale in an order that shows how the names of the scale degrees were derived. The curved lines above the staff show the intervallic distance between each scale degree and the tonic.
- The word dominant is inherited from medieval music theory, and refers to the importance of the fifth above the tonic in diatonic music.
- The word mediant means “middle,” and refers to the fact that the mediant is in the middle of the tonic and dominant pitches.
- The Latin prefix super means “above,” so the supertonic is a second above the tonic. This is the only “super-” interval.
- The Latin prefix sub means “below”; the subtonic, submediant, and subdominant are the inverted versions (i.e., below the tonic) of the supertonic, mediant, and dominant respectively. (Note that in this text, we prefer the term leading tone instead of “subtonic” when referring to the scale-degree that is a half step below tonic, so named because it is often thought of as “leading” toward the tonic.)
Key Signatures
A key signature, consisting of either sharps or flats, appears at the beginning of a composition, after a clef but before a time signature. You can remember this order because it is alphabetical: clef, key, time. Example 7 shows a key signature in between a bass clef and a time signature.


Key signatures collect the accidentals in a scale and place them at the beginning of a composition so that it is easier to keep track of which notes have accidentals applied to them. In Example 7, there are flats on the lines and spaces that indicate the notes B, E, and A (reading left to right). Therefore, every B, E, and A in a composition with this key signature will be flat, regardless of octave. In Example 8 both of these Bs will be flat because B♭ is in the key signature.
Flat key signatures have a specific order in which flats are added, and the same is true of the sharps in sharp key signatures. These orders apply regardless of clef. Example 9 shows the order of sharps and flats in all four clefs that we have learned:

The order of sharps is always F, C, G, D, A, E, B. This can be remembered with the mnemonic “Fat Cats Go Down Alleys (to) Eat Birds.” The sharps form a zig-zag pattern, alternating going down and up. In the treble, bass, and alto clefs, this pattern “breaks” after D♯ and then resumes. In the tenor clef, there is no break, but F♯ and G♯ appear in the lower octave instead of the upper octave.
The order of the flats is the opposite of the order of the sharps: B, E, A, D, G, C, F. This makes the order of flats and sharps palindromes. The order of flats can be remembered with this mnemonic: “Birds Eat And Dive Going Copiously Far.” The flats always make a perfect zig-zag pattern, alternating going up and down, regardless of clef, as seen in Example 9.
There are easy ways to remember which key signature belongs to which major scale. In sharp key signatures, the last sharp is a half step below the tonic (the first note of a scale). Example 10 shows three sharp key signatures in different clefs. Here’s how to identify each with this method:

- The last sharp (in this case the only sharp), F♯, is a half step below the note G. Therefore, this is the key signature of G major.
- The last sharp, G♯, is a half step below the note A. Therefore, this is the key signature of A major.
- The last sharp, E♯, is a half step below the note F♯. Therefore, this is the key signature of F♯ major.
In flat key signatures, the second-to-last flat is the tonic (the first note of a scale). Example 11 shows three flat key signatures in different clefs. Here’s how to identify each with this method:

- The second-to-last flat in this key signature is B♭. Therefore, this is the key signature of B♭ major.
- The second-to-last flat is A♭. Therefore, this is the key signature of A♭ major.
- The second-to-last flat is G♭. Therefore, this is the key signature of G♭ major.

There are two key signatures that have no “tricks” that you will simply have to memorize. These are C major, which has nothing in its key signature (no sharps or flats), and F major, which has one flat: B♭ (Example 12).
Example 13 shows the key signature for C major (no sharps or flats) followed by all of the sharp key signatures in order in all four clefs: G, D, A, E, B, F♯, and C♯ major.

Example 13. The key signatures of C, G, D, A, E, B, F♯, and C♯ in all four clefs.
Example 14 first shows the key signature for C major (no sharps or flats), then all of the flat key signatures in order in all four clefs: F, B♭, E♭, A♭, D♭, G♭, and C♭ major.

Example 14 first shows the key signature of C major (with no sharps or flats), and then the key signatures of F, B♭, E♭, A♭, D♭, G♭, and C♭ in all four clefs.
There is one other “trick” that might make memorization of the key signatures easier: C major is the key signature with no sharps or flats, C♭ major is the key signature with every note flat (7 flats total), and C♯ major is the key signature with every note sharp (7 sharps total).
Major keys are said to be “real” if they correspond to one of the key signatures in Examples 13 or 14. If a double sharp or double flat would be needed for a key signature, then that key signature would be “imaginary.” Occasionally, you may encounter music in an imaginary key. Example 15 shows an F♭ major scale; an F♭ major key signature is imaginary because it would need a B𝄫.
https://musescore.com/user/32728834/scores/6817049/embed
Example 15. An F♭ major scale in treble clef.
The Circle of Fifths
The circle of fifths is a convenient visual. In the circle of fifths, all of the major key signatures are placed on a circle in order of number of accidentals. The circle of fifths is so named because each key signature is a fifth away from the ones on either side of it. Example 16 shows the circle of fifths for major key signatures:
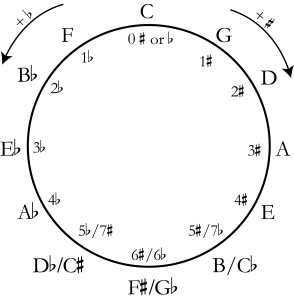
If you start at the top of the circle (12 o’clock), the key signature of C major appears, which has no sharps or flats. If you continue clockwise, sharp key signatures appear, each subsequent key signature adding one more sharp. If you continue counter-clockwise from C major, flat key signatures appear, each subsequent key signature adding one more flat. The bottom three key signatures (at 7, 6, and 5 o’clock) in Example 16 are enharmonically equivalent. For example, the B major and C♭ major scales have different key signatures—five sharps and seven flats, respectively—but they sound the same because the notes B and C♭ are enharmonically equivalent.
- Major Scales Tutorial (musictheory.net)
- Major Scales (Practical Chords and Harmonies)
- Major Scales (YouTube)
- Scale Degree Names (musictheoryfundamentals.com)
- Scale Degree Names (musictheory.net)
- Solfège History and Tutorial (Earlham College)
- Scale Degrees, Solfège, and Scale-degree Names (YouTube)
- Major Key Signatures (musictheory.net)
- Sharp Key Signatures (YouTube)
- Flat Key Signatures (YouTube)
- Major Key Signature Flashcards (music-theory-practice.com)
- The Circle of Fifths (YouTube)
- The Circle of Fifths (Classic FM)
- Writing Major Scales (.pdf), from Tonic and Other Scale Degrees (.pdf)
- Writing Major Key Signatures (.pdf)
- Identifying Major Key Signatures (.pdf)
- Major Keys Worksheets for Children (.pdf)
- Scale Degrees or Solfège (.pdf, .pdf)
An indication of meter in Western music notation, often made up of two numbers stacked vertically.
Vertical lines that create measures.
[["Chord","Has common tones with...","#colspan#","#colspan#","#colspan#","#colspan#","#colspan#","#colspan#","#colspan#"],["i","III","III+([latex]\\uparrow\\hat7[/latex])","iv","IV ([latex]\\uparrow\\hat6[/latex])","v","V ([latex]\\uparrow\\hat7[/latex])","VI","vi\uea97 ([latex]\\uparrow\\hat6[/latex])"],["ii\uea97","iv","","v","I ([latex]\\uparrow\\hat6[/latex])","VI","","VII","vii\uea97 ([latex]\\uparrow\\hat7[/latex])"],["ii","","","","","","","",""],["iii ","I","","V","","vi","","","vii\uea97"],["III+","","","","","","","",""],["iv","I","","ii","","vi","","","vii\uea97"],["IV","","","","","","","",""],["v","I","","ii","","iii","","","vii\uea97"],["V","","","","","","","",""],["VI ","I","","ii","","iii","","","IV"],["vi\uea97","","","","","","","",""],["VII ","ii","","iii","","IV","","","V"],["vii\uea97","","","","","","","",""]]
Key Takeaways (In Progress)
- The harmonic series is fundamental in understanding tone color, harmonic structures, and the nature of tonality.
- The relationship of a tone within the harmonic series to the fundamental can be indicated by its frequency of occurrence.
- The perfect fifth is the most stable interval after the octave and forms a pivotal relationship within the harmonic series.
- Scale degrees in major and minor modes have specific names and functions, with a focus on the relationships of the perfect fifth interval.
- Each scale degree has an associated upper and lower perfect fifth relationship, creating a dynamic tension in tonal music and attendant harmonic progressions.
- The progression of music is cyclical: The Tonic leads to the SubDominant, which gravitates towards the Dominant, eventually returning to the Tonic.
- There are three pivotal tonal regions: Tonic (stable), SubDominant (restless), and Dominant (unstable).
- The progression in tonal regions can be represented on the Circle of Fifths, reflecting the flow of "tonal gravity".
The Harmonic Series and the Perfect Fifth
Drawing from foundational studies in musicianship and music fundamentals, one realizes the profound significance of the harmonic series in the realm of music. Not only is it pivotal in shaping our perception of tone color (timbre), but it also lays the groundwork for understanding harmonic structures like chords and the nature of tonality. Broadly speaking, as one progresses up the harmonic series from a given fundamental, the tonal relationship with the fundamental becomes more distant. Moreover, the frequency with which a tone recurs within the series can be viewed as an indicator of its relationship or kinship with the fundamental — the most recurrent tone in the series.

To illustrate, in Figure 1 where C serves as the fundamental, the first thirteen overtones reveal C four times, more than any other tone in this overtone set (up to the 14th harmonic). Following C, G makes its appearance thrice, and subsequently, E is seen twice, and the pattern continues. From this observation, one can infer that G holds the most harmonious relationship to C, the fundamental, with E trailing closely behind.
Given that G shares the closest tonal affinity with C, and the interval between C and G is a perfect fifth, it stands to reason that the perfect fifth emerges as the most stable interval, second only to the octave. This interval encapsulates a pivotal relationship within the harmonic series. Observing the fifth relationships starting from C, as depicted in Figure 1, we find a sequence: C-G-D-A, with E up next. This interval, accompanied by the array of tones more distantly related to the fundamental, underpins our comprehension of expansive harmonic relationships in tonal music.
Tonal Scale Degree Function: Major Mode
Before delving further, let's briefly review the scale degrees in the major mode and their associated names:

ABBREVIATION |
NAME |
| T [latex](\hat1)[/latex] | TONIC |
| ST [latex](\hat2)[/latex] | SUPERTONIC |
| M [latex](\hat3)[/latex] | MEDIANT |
| SD [latex](\hat4)[/latex] | SUBDOMINANT |
| D [latex](\hat5)[/latex] | DOMINANT |
| SM [latex](\hat6)[/latex] | SUBMEDIANT |
| LT [latex](\hat7)[/latex] | LEADING-TONE |
Scale Degree Relationships
Each scale degree, barring two exceptions, has an upper and lower perfect fifth interval relationship. These are defined by the harmonic series and are associated with two other scale degrees. Another perspective on these relationships views them as sets of relative Dominants and SubDominants for each scale degree. The Dominant is defined as a tone a perfect fifth above a given fundamental note, while the SubDominant lies a perfect fifth below. We can explore each of these relationships in the major mode in detail.
Tonic-Dominant & Dominant-SuperTonic

The foremost and most pivotal of these perfect fifth "polarities" is established on the Tonic scale degree [latex](\hat1)[/latex]. A crucial concept to understand is the inherent desire of the Dominant tone, located a fifth above, to resolve to or merge with the Tonic. This inclination is rooted in the harmonic series. Likewise, the Tonic gravitates towards the SubDominant, situated a perfect fifth below. Figure 3 illustrates this in the key of C major, with the flow of tones moving downward by perfect fifths, denoted by red arrows. The term "SubDominant" translates to "lower Dominant." As such, the SubDominant continuously draws the Tonic towards it, making it the most potent tone in the mode due to the natural laws of the harmonic series. This dynamic tension—between the Dominant's pull to the Tonic and the Tonic's attraction to the SubDominant—creates the fundamental ebb and flow in tonal music's harmonic progressions.
Expanding on this, the second most vital polarity in the mode involves the Dominant. When viewed locally, the Dominant, while sounding, takes on the role of a secondary Tonic. It naturally has its upper perfect fifth counterpart, the SuperTonic, wanting to bond with it. Similarly, as previously discussed, it wishes to move to and merge with the Tonic.
SuperTonic-SubMediant & SubMediant-Mediant

Moving on, if we treat the SuperTonic as a localized tonic when sounded, it possesses an upper Dominant, the SubMediant, that seeks to resolve to it. Following this logic, the Dominant functions as the lower fifth SubDominant.
SubDominant-Mediant

Concluding, we examine the relationships around the SubDominant and the Mediant. In the SubDominant's case, we recognize the already familiar upper relative Dominant as the Tonic, which tends to descend to the SubDominant. However, the major mode's SubDominant does not possess a lower SubDominant perfect fifth. Therefore, within any major key, the SubDominant acts as a kind of boundary, preventing forward movement without modulating (changing the key or mode). Likewise, for the Mediant, a stable relative Dominant does not exist since the Leading-Tone lacks a consistent fifth as part of its harmony, being either the diminished triad or diminished seventh chord.
Tonal Scale Degree Function: Minor Mode
Moving forward to the minor mode, let's delve into the scale degree functions in the natural minor:
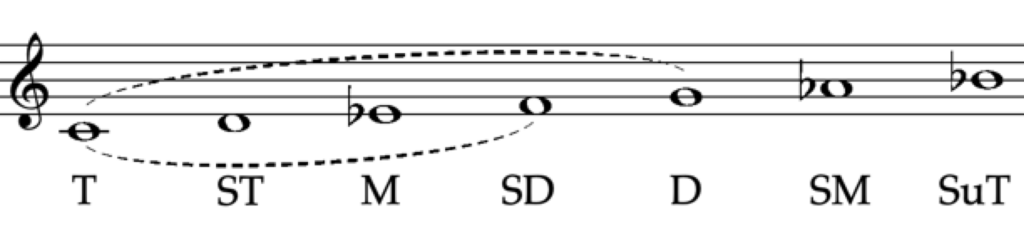
ABBREVIATION |
NAME |
| T [latex](\hat1)[/latex] | TONIC |
| ST [latex](\hat2)[/latex] | SUPERTONIC |
| M [latex](\hat3)[/latex] | MEDIANT |
| SD [latex](\hat4)[/latex] | SUBDOMINANT |
| D [latex](\hat5)[/latex] | DOMINANT |
| SM [latex](\hat6)[/latex] | SUBMEDIANT |
| SuT [latex](\hat7)[/latex] | SUBTONIC |
Scale Degree Relationships
Similar to the major mode, we can explore the relationships in the upper and lower perfect fifth polarities in the minor mode. Notably, some variations exist due to the two different forms of minor, which cause slight alterations in the relationships. The quality of the chords—whether major or minor (excluding any unstable diminished chords)—is secondary. The primary focus is on the interval relationships between scale degrees. For instance, the function of the Dominant in the minor mode remains consistent, even though the quality of the chords built on the Dominant can shift from minor to major depending on the form of minor (Natural-Descending or Ascending). Let's examine some specifics:
Tonic-Dominant & Dominant-SuperTonic Relationships

The Tonic polarity (from Tonic up to Dominant and down to SubDominant) is consistent with the major mode. However, in the natural form of minor, the Dominant polarity varies as the SuperTonic lacks stable harmony due to the diminished chord typically built on it. This changes in the ascending form of the minor (Melodic), where a stable SuperTonic minor triad emerges:
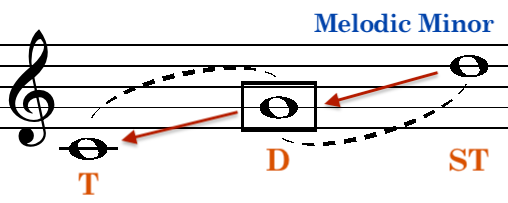
SubDominant-Tonic & SubTonic-SubDominant Relationships

In natural minor, a stable SubTonic introduces a new polarity: SubDominant-Tonic. Here, the SubDominant feels a gravitational pull downwards to the SubTonic. Additionally, the SubTonic-SubDominant polarity arises, where the SubTonic is drawn towards the SubMediant.
Mediant-SubTonic & SubMediant-Mediant Relationships

The Mediant-SubTonic polarity emerges, where the Mediant feels drawn to the SubMediant. With the SubMediant-Mediant polarity, the lack of a stable SuperTonic prevents a downward pull from the SubMediant. One might wonder if, in the ascending form, the raised SuperTonic creates a stable relationship with the SubMediant. It is a good question; however, despite the presence of a stable SuperTonic in the ascending form of the minor, the SubMediant does not establish a strong gravitational pull towards it. The raised 6th and 7th scale degrees introduce a different melodic and harmonic context, altering our perception of the inherent relationships.
Harmonic Function in Tonality
Having revisited the scale degrees in major and minor modes and examined the profound influence of the perfect fifth relationships among these degrees, we can broaden our view to encompass the concept of tonal harmonic function. In essence, there are three pivotal tonal regions:
- Tonic Region: Stable and at rest, it reinforces the key/tonal center.
- SubDominant Region: Restless and in contrast with the key/tonal center, it evokes a sense of movement.
- Dominant Region: The most unstable region, it exhibits a compelling pull towards the Tonic region, playing a crucial role in maintaining the balance of the key/tonal center.
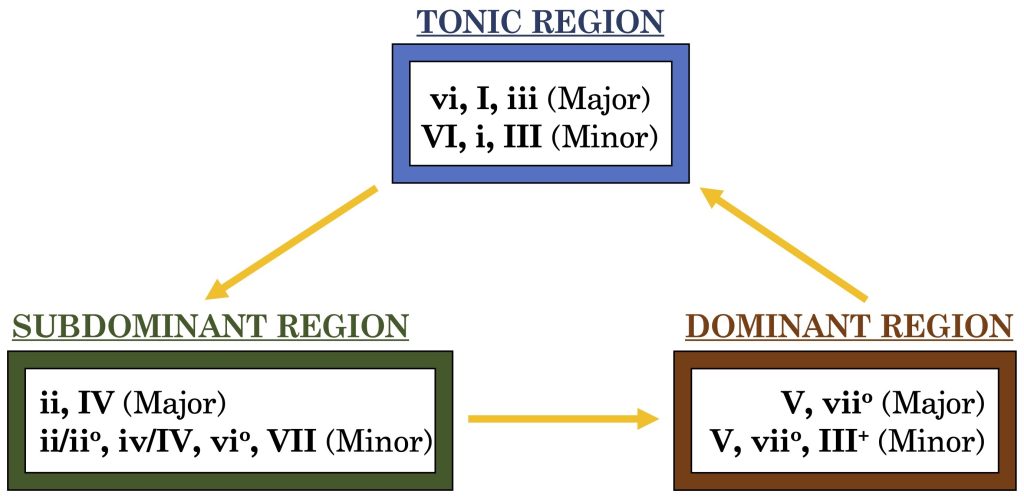
Figure 11 presents a flowchart that delineates each of the three tonal regions. The yellow arrows indicate the harmony's propensity to transition between these regions. Notably, the chart's counter-clockwise orientation mirrors its representation on the Circle of Fifths, underscoring the progression in descending fifths through the scale degrees.
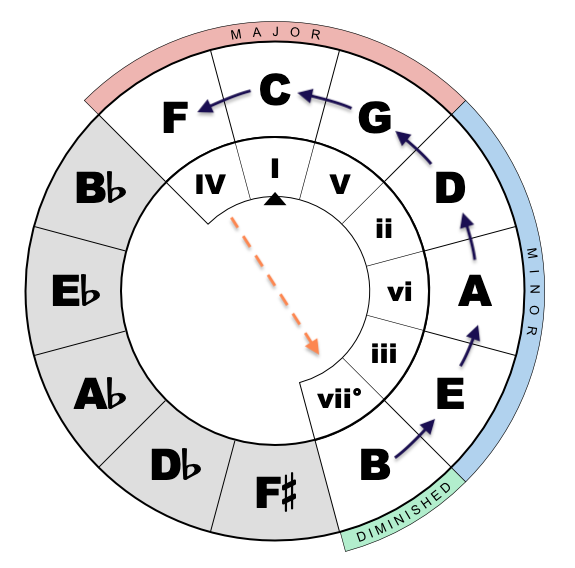
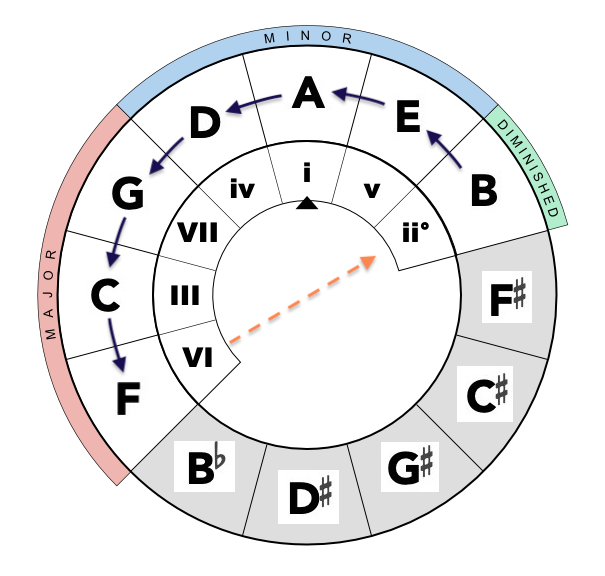
It's important to recognize that at a certain juncture across the circle, the pattern doesn't maintain a stable perfect fifth, depicted by the dashed yellow line.
Reflecting upon our journey through music theory, we can recollect:
- The harmonic series substantiates the perfect fifth and the downward pull from Dominant to Tonic, alongside the analogous pulls of the secondary scale degrees.
- The progression is cyclical: The Tonic leads to the SubDominant, which subsequently gravitates towards the Dominant, eventually returning to the Tonic.
Harmonic Progression: The Root Motion
Strong Harmonic Progressions
Weak Harmonic Progressions
Adjacent Root Motion
Harmonic Progression: The Sub-Phrase
Composite harmonic motion, building sub-phrases.
RWU EXERCISES
TBD
Schoenberg Theory of Harmony Examples
Further Reading
- Schoenberg, Arnold: Theory of Harmony
- Schoenberg, Arnold: Structural Functions of Harmony
Perfect Unison
"Bright" refers to a more major sound, while "dark" refers to a more minor sound.
A diatonic mode that follows the pattern W–W–H–W–W–W–H. This is equivalent to a major scale.
Imitation sees two or more parts enter separately with (versions of) the same melody.

