Chapter 10: Rotational Motion

Adria Updike

10 Chapter 10: Rotational Motion

Section 10.1: Uniform Circular Motion

Textbook Section 4.4: Uniform Circular Motion

Textbook Section 10.1: Rotational Variables

Uniform Circular Motion refers to motion in a circular path at a constant speed. Examples of this include carousels, racetracks, and stellar orbits. Rotational motion refers to objects moving in a circle around a central point, and translational motion refers to motion in a straight line. You can combine these types of motion; for example, putting a spin on a football as you throw it.

The circumference of a circle is the distance around the edge, and is calculated as $C = 2 \pi r$ where $r$ is the radius of the circle. The angle through which a clock hand might move is given at $\theta = s/r$ , where $s$ is some arc length (distance swept out by the tip of the clock hand in some given time interval).

A radian is defined at 360 $^{\circ}$ of a circle divided by $2\pi$ , or 57.3 $^{\circ}$ . $2\pi$ radians are equivalent to one revolution (one full trip around the circle and back to your starting place).

The angular velocity of an object moving in a circular path tells you how many $\theta$ you move through in a certain time period, and is calculated as:

$\omega_{av,z} = \frac{\Delta \theta}{\Delta t}.$

This is the average angular velocity of an object spinning in the $x-y$ plane (the direction of the angular velocity is perpendicular to the plane, or in the direction of $z$ ). Instantaneous angular velocity $\omega_z$ is found as following:

$\omega_z = \lim_{\Delta t \to 0} \frac{\Delta \theta}{\Delta t} = \frac{d \theta}{d t}$

The units of angular velocity are given in radians per second (rads/s). The angular displacement of an object moving in a circular path is given by $\Delta \theta = \theta_f - \theta_i$ .
Note that $\Delta \theta$ can be a number larger than 2 $\pi$ ! Typically when moving in a circle, we start over when we reach our starting point again, but not when calculating angular displacements.

Clockwise motion (cw) around a circle gives us a negative angular velocity, and counterclockwise motion (ccw) gives us a positive angular velocity. We assume for now that our rotating objects are rigid bodies (do not deform, bend, or stretch while moving in a circle) and that every point on the object has the same angular velocity.

Angular distance $\theta$ can be given at $\theta = s/r$ , and velocity is equivalent to $v = d/t$ . We can re-write the former equation as $s = \theta r$ , and plug into the latter to receive $v = \theta r/t = \omega r$ . Now we can relate translational (also called linear) velocity $v$ and our angular velocity $\omega$ if we know the radius of the circle traced out by our object.

Section 10.2: Centripetal Acceleration and Force

As an object moves around a circular path, the magnitude of its velocity can remain constant, but the direction is constantly changing, so it is undergoing an angular acceleration. This acceleration due to an object moving in a circular path at a constant speed is called centripetal acceleration, and is given by:

$a_c = \frac{v^2}{r} = r w^2$

Textbook Section 6.3: Centripetal Force

The force causing this acceleration is the centripetal force. Note that this is NOT a new force! It’s not magically arising out of the fact that something travels in a circle. The centripetal force was already on your diagram in some form — it may be the friction force, or the tension force, or even a gravitational force.

Section 10.3: Rotational Kinematics

Textbook Section 10.2: Rotation with Constant Angular Acceleration

When an object moves in a circular path and the speed is changing as well as the direction, we say the object is undergoing an angular acceleration, given in units of rad/s $^2$ . The average angular acceleration is calculated as:

$\alpha_{av,z} = \frac{\Delta \omega_z}{\Delta t}$

and the instantaneous angular acceleration is found as:

$\alpha_z = \frac{d}{dt} \left( \frac{d \theta}{d t} \right) = \frac{d \omega_z}{dt} = \frac{d^2\omega}{dt^2}.$

If $\omega$ is increasing, then $\alpha$ must be in the same direction as $\omega$ . If $\omega$ is decreasing, the opposite must be true.

We can use the same kinematics equations for angular coordinates as we do for linear motion. Simply substitute the values to get the equations below.

$\omega_z = \omega{0,z} + \alpha_z t$

$\omega_z^2 = \omega_{0,z}^2 + 2 \alpha_z \Delta \theta$

$\Delta \theta = \omega_{0,z} + \frac{1}{2} \alpha_z t^2$

Textbook Section 10.3: Relating Angular and Translational Quantities

Section 10.4: Center of Mass

Textbook Section 9.6: Center of Mass

As we start dealing with objects that aren’t entirely located at a single point in space (point particles) and deal instead with extended objects, we want to simplify our calculations by pretending that extended objects are located at a single location, like a point particle. That location, where we can pretend all the mass of an extended object is located, is called the center of mass (or center of gravity) of our object. For a uniform, symmetric object (like a sphere), the center of mass is in the middle of the object. That’s the average location of all the mass in the object.

To calculate the center of mass of an object or collection of objects, use the following formulas in the $x$ and $y$ directions (can also be generalized to the $z$ direction):

$x_{cm} = \frac{\sum\limits_{i=1}^N m_i \, x_i}{\sum\limits_{i=1}^N m_i} \hspace{.5in}$

$y_{cm} = \frac{\sum\limits_{i=1}^N m_i \, y_i}{\sum\limits_{i=1}^N m_i} \hspace{.5in}$

Note that the designation $x_{cm}$ and $y_{cm}$ means “center of mass”, not “centimeters”! In each case, we are summing over the location of each individual object (it’s own center of mass, located at the coordinates ( $x_i, y_i$ ) and it’s mass, $m_i$ .

Section 10.5: Moment of Inertia

Textbook Section 10.4: Moment of Inertia and Rotational Kinetic Energy

Our moment of inertia $I$ was defined in Chapter 9 in terms of the torque, $\tau$ . We found that $\tau = I \alpha$ , and we could write $I$ for a collection of point particles as

$I = \sum_i m_i r_i^2$

where $m_i$ is the mass of a point particle and $r_i$ is the distance between the point particle and the axis of rotation (pivot point). Calculating $I$ for more extended objects than point particles require us being careful as to which axis we are considering. All lines drawn through a point particle are identical, but you can draw different lines through a cylinder and rotate it around different axes of rotation, changing its particle distribution from the axis and thus its moment of inertia.

You can find the moment of inertia for various object configurations in your textbook. A few are listed on the next page. To construct an object made up of many discrete pieces, each of which has its own moment of inertia, you merely add the moments of inertia of all the pieces. You will never have a negative moment of inertia.

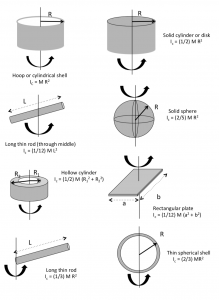
What if you want to use an axis not given in your table? Take a look at the solid sphere in the left bottom corner of the diagram on the previous page. What if you wanted to put the axis of rotation not through the center of the sphere, but through an edge of the sphere? That’s when you need the parallel axis theorem. The parallel axis theorem tells you how to modify your given, center of mass moment of inertia for an object in order to rotate the same object through a different axis.

$I_{pp} = I_{cm} + M d^2$

You begin the parallel axis theorem using the given center of mass moment of inertia from the table for that shape, and simply add on another term that involves the mass of the object times the square of the distance between the new axis and the axis used in the center of mass moment of inertia. For the example given, our new moment of inertia for our sphere rotating around an edge instead of the center would be $I_{pp} = 2/5 \,\, M R^2 + M R^2$ because the mass of the sphere is $M$ and the distance between the axis used in the picture and the edge of the sphere is another factor of the radius $R$ .

Section 10.6: Rotational Kinetic Energy

Textbook Section 10.4: Moment of Inertia and Rotational Kinetic Energy

The rotational kinetic energy is the energy associated with an object due to its rotation around an axis. This is why we have previously avoided the examples of objects rolling downhill and instead used objects sliding down hills. Objects sliding do not rotate and only have translational (regular) kinetic energy ( $KE_t$ ), while rotating objects have rotational kinetic energies ( $KE_r$ , and balls rotating while rolling down a hill have a combination of rotational and translational kinetic energy.

The rotational kinetic energy, $KE_R$ , is written as

$KE_{rot} = \frac{1}{2} I \omega^2$

where $I$ is the moment of inertia of the rotating object and $\omega$ is its rotational velocity.

The total kinetic energy of a rotating object can therefore be written as

$KE = \frac{1}{2} m v^2 + \frac{1}{2} I \omega^2$

Do not confuse $\omega$ with $v$ ! While they are related, $v$ and $\omega$ are not the same quantity. To exchange one for another, use $v = r \omega$ .

Section 10.7: Torque

Textbook Section 10.6: Torque

Just as we had rotational equivalents of the position (radians), velocity (angular velocity), acceleration (angular acceleration), and mass (moment of inertia), we have a rotational equivalent of force called the torque. Just as a force causes an acceleration, a torque causes an angular acceleration. Just as the terms for linear motion could be transformed into the rotational motion terms by multiplying by the distance from the rotation axis $r$ , the torque is simply a force applied at some distance from the rotation axis. The torque is given the following formula, and is expressed as the symbol $\tau$ :

$\vec{\tau} = \vec{r} \cross \vec{F} = r \, F \, \rm{sin}(\theta)$

where the first expression for the torque is the cross product, or vector product, of two vectors. The cross product is found by multiplying the perpendicular components of a vector, and results in another vector.

The torque can also be expressed in terms of the rotational equivalent of the formula $F = ma$ , as:

$\tau = I \alpha$

.

When multiple forces applied to an object, we drew a free body diagram and found the sum of the forces, a net force. We’ll do the same thing with multiple torques working on an object to find the net torque on the object.

$\Sum \tau = \Sum I \alpha = \Sum r F \rm{sin}(\theta)$

This leads us to a second requirement for equilibrium. Where we initially defined equilibrium as a net force on an object of zero, now we will also add the condition that the net torque on the object must be equal to zero.

Section 10.8: The Cross Product

Textbook Section 2.4: Products of Vectors

When taking the cross product (also called the vector product) of two vectors, there are two ways you can calculate it. If you have two vectors in magnitude and direction notation, you can simply take the cross product by multiplying the magnitudes of the vectors times the angle between them.

$\vec{A} \cross \vec{B} = A \, B \, \rm{sin}(\theta)$

However, if you have two vectors in $\hat{i}, \hat{j}, \hat{k}$ notation, you need to use the following formula to find the vector cross product.

$\vec{A} \cross \vec{B} = (A_y B_z - A_z B_y) \hat{i} + (A_z B_x - A_x B_z) \hat{j} + (A_x B_y - A_y B_x) \hat{k}$

In Class Group Problem 10.1:

A ladybug sitting on the edge of a rotating record player moves through 3.5 revolutions in 0.35 s. What is the angular velocity of the insect?

The record player now has an angular displacement described by $\theta(t) = (3.2$ rad/s $) t + (0.8$ rad/s $^3) t^3$ . How far (in linear distance) has the ladybug traveled after 5 s if it is sitting 5.0 cm from the rotation axis? Hint: don’t take the derivative to find the angular velocity, we don’t have a constant acceleration. Find another way to solve this.

In Class Group Problem 10.2:

A car wheel has a radius of 21 cm and is rotating at 700 rpm (revolutions per minute). What is the linear velocity of the car (how fast is it moving)?

In Class Group Problem 10.3:

(a) A DVD put in your DVD player accelerates from an angular velocity of 300 rpm to spinning at 1530 rpm in 3.50 seconds. What is the angular acceleration of a point on the DVD?

(b) If the DVD had that same constant angular acceleration from rest, how many meters had a point 2.3 cm from the center rotated through after 1.7 seconds?

In Class Group Problem 10.4:

You are driving down I-95 South at 60 mph and decide to get off at an exit. The exit ramp is flat with a radius of curvature of 75 m. You are in a hurry, so you ignore the reduced speed limit signs on the ramp.

(a) What is the centripetal force experienced by your 800 kg car?

(b) The centripetal force on your car is due to the force of static friction between the wheels and the ground. Draw the free body diagram for the car as it goes around the curve and determine the required coefficient of static friction required to keep the car on the flat ramp.

(c) The coefficient of static friction between rubber wheels and concrete is 1.0 under dry conditions. Do you successfully negotiate the curve? What would have happened if you didn’t, and why?

(d) The coefficient of static friction between rubber wheels and concrete is 0.7 under wet conditions. What is the maximum safe speed in mph for this exit ramp when it is raining?

(e) Many exit ramps are banked curves, not flat. Draw a free body diagram for your car on a curve banked at 15 $^{\circ}$ . Assume the force of static friction points $\emph{down}$ the ramp. Recall that the centripetal force points perpendicular to gravity towards the center of the circle your car is driving in – in this case, we don’t want to rotate our coordinate system.

(f) Write the sum of your forces in the $x$ and $y$ directions and break your friction and normal forces into components. Recall that the centripetal force points perpendicular to the gravitational force, towards the center of the circle the car is making. Calculate the maximum safe speed in mph on a wet exit ramp banked at 15 $^{\circ}$ .

(g) Which curve is safer to navigate – a flat or banked curve? Why?

(h) An $\emph{ideally}$ banked curve removes friction entirely and replaces it with the $x$ -component of the normal force. Calculate the ideally banked curve angle for which a car moving at 60 mph will experience no friction.

(i) Why don’t we bank all exit ramps this way?

In Class Group Problem 10.5:

A dog door (hinged at the top, free to swing) is 0.500 m tall. A dog applies a horizontal force of 3.50 N with his head 0.200 m up from the bottom of the door. What is the torque experienced by the door?

In Class Group Problem 10.6:

Find the cross product of $\vec{r}$ and $\vec{F}$ .

$\vec{r}$ = (5.2 m) $\hat{i}$ – (2.8 m) $\hat{j}$ + (8.4 m) $\hat{k}$

$\vec{F}$ = (-7.1 N) $\hat{i}$ – (3.6 N) $\hat{j}$ + (2.4 N) $\hat{k}$

In Class Group Problem 10.8:

Two brothers are playing on a seesaw 6.0 m long with an axis of rotation through the middle. One brother (35 kg) sits 1.2 m from the left edge of the seesaw.

(a) Where does his 27 kg brother need to sit in order to balance the seesaw? Give your answer as the distance from the left side of the seesaw.

(b) The brothers move the seesaw support so that now it rests 2.5 m from the left side, not exactly in the middle. The 35 kg brother now sits 1.5 m from the left side. Where does the 27 kg brother need to sit to balance the seesaw this time if the seesaw has a mass of 10 kg? Give your answer as the distance from the left side of the seesaw.

(c) What are the moments of inertia of the brothers in part (b) if we treat them as point particles and if the 27 kg brother sits at 5.5 from the left side of the seesaw?

(d) What angular acceleration does the seesaw undergo in the case of part (c)?

(e) Assume the right end of the seesaw is 0.38 m off the ground when perfectly balanced. How long does it take the right end of the seesaw to hit the ground after the 27 kg brother takes his place in part (c)?

In Class Group Problem 10.9:

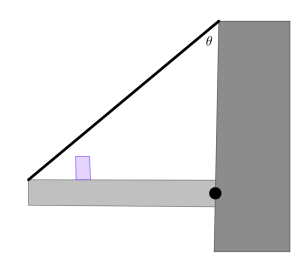
The plank below is 5.8 m long, 130 kg, and attached to the wall by a hinge on the right that allows it to rotate. A box sits on the plank 3.7 m from the left end of the plank, and a rope is attached to the plank at 0.9 m from the left end of the plank. The rope makes an angle of 34 $^{\circ}$ with the plank as shown below. If the maximum tension the rope can take without breaking is 1900 N, what is the maximum mass of the box the plank can support?

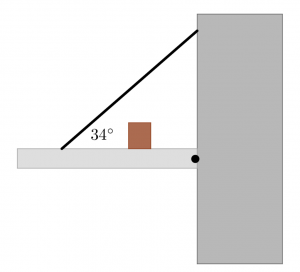
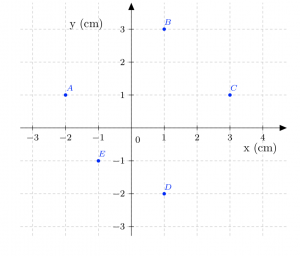
In Class Group Problem 10.10:

Find the center of mass of the following arrangement of point particles if the masses are: $m_A$ = 1.0 kg, $m_B$ = 0.75 kg, $m_C$ = 2.4 kg, $m_D$ = 0.50 kg, and $m_E$ = 3.1 kg.

In Class Group Problem 10.11:

Two balls of radius 2.5 cm and mass 2.0 kg sit motionless at the top of an incline 3.0 m long at an angle of 15 $^{\circ}$ to the horizontal. When released, what are their velocities at the bottom of the ramp? Which one reaches the bottom first? One ball is a hollow shell, the other is a solid sphere.

In Class Group Problem 10.12:

Calculate the moment of inertia of the following object around the $x$ -axis. Assume all masses are point particles connected by massless rods, and that $m_A$ = 3.0 kg, $m_B$ = 2.0 kg, $m_C$ = 4.5 kg, $m_D$ = 1.2 kg, and $m_E$ = 5.4 kg.

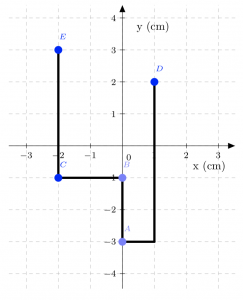
Now calculate the moment of inertia of the same object around the $y$ -axis.

In Class Group Problem 10.13:

For Halloween this year, you decide to go as Thor, Norse God of Thunder. You have made yourself a replica of Thor’s hammer out of two pieces of hollow copper pipe ( $\rho$ = 8.96 g/cm $^3$ ). The top piece has an exterior diameter of 5 inches, an interior diameter of 4.5 inches, and a length of 7 inches. The bottom pipe has an exterior diameter of 1 inch, an interior diameter of 0.5 inches, and a length of 10 inches.

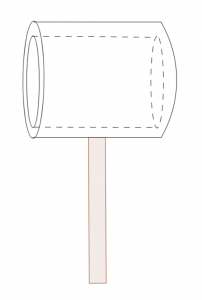
(a) What are the masses of each of the two sections of the hammer?

(b) What is the moment of inertia of this hammer if you swing it in a circle that leaves the bottom end of the hammer fixed in place and the top end coming out of the page and then back into it again?

(c) What is the moment of inertia of the hammer if do the above motion while the top part of the hammer is also spinning around the axis that goes through the center of the top pipe?

(d) Calculate the rotational kinetic energy of the hammer in the previous part if it completes 4 total revolutions about the $x$ -axis in 10 seconds.

In Class Group Problem 10.15:

The automatic flag raising system on a horizontal flag pole attached to the vertical outside wall of a tall building has become stuck. The management of the building wants to send a person crawling out along the flagpole to fix the problem. Because of your physics knowledge, you have been asked to consult with a group to decide whether or not this is a good idea. You are all too aware that no one could survive the 250 foot fall from the flagpole to the ground. The flagpole is a uniform 120 lb steel beam which is very strong and rigid. One side of the flagpole is attached to the wall of the building by a hinge so that it can rotate vertically. Nine feet away, the other end of the flagpole is attached to a strong, lightweight cable. The cable goes up from the flag pole at an angle of 35 $^{\circ}$ until it reaches the building where it is bolted to the wall. The mechanic who will climb out on the flag pole weighs 150 lbs. including equipment. You know that the maximum tension the cable holding the flagpole can take is 500 lbs.

If the mechanic can only fix the flagpole mechanism by crawling all the way out to the end of the flagpole, will the cable hold?

A simple yes/no will not sufficiently answer this question. You must support your answer with your calculations.

In Class Group Problem 10.16:

Because of your physics background, you have been asked to be a stunt consultant for a motion picture about a genetically engineered prehistoric creature that escapes from captivity and terrorizes the city. The scene you are asked to review has the three main characters of the movie being chased by the creature through an old warehouse. At the exit of the warehouse is a thick steel fire door 10 feet high and 6.0 feet wide weighing about 2,000 lbs. In the scene, the three actors are to flee from the building and close the fire door (initially at rest), thus sealing the creature inside the building. With the creature running at 30 mph, they have 5.0 seconds to shut the door. You are asked to determine if they can do it. You estimate that each actor can each push on the door with a force of 50 lbs. When they push together, each actor needs a space of about 1.5 feet between them and the next actor. The door, which has a moment of inertia of 1/3 M L $^2$ around its hinges, needs to rotate 120 degrees for it to close completely.

Practice Exam Question 10.1: