13 Chapter 14: Fluid Mechanics
Textbook Chapter 14: Fluid Mechanics
Section 14.1: Fluids
There are three main phases of matter we explore in this chapter. A solid is a material with a definite shape and volume, with atoms close together and chemically bound. A liquid has fewer bonds between nearby atoms and can change its shape, but not its volume. Liquids are incompressible; they cannot be forced into a smaller volume than they normally inhabit. A gas has no bonds between nearby particles, no definite volume and takes the shape of its container. Gasses can be compressed. Both gasses and liquids are consider fluids; solids are not fluids.
Materials in a definite shape, volume, or container can be characterized by a density equal to the mass of the material divided by its volume, as we see in Equation 1. Density is represented by the Greek letter ![]() (rho) and has units of kg/m
(rho) and has units of kg/m![]() .
.
![]()
Section 14.2: Pressure
Textbook Section 14.1: Fluids, Density, and Pressure
Textbook Section 14.2: Measuring Pressure
When a fluid is contained in a volume, the particles in the fluid move around and hit each other and the sides of the container. The pressure of a fluid in a container or on an object is due to the particles in the fluid colliding with the sides of the container or object. As they hit the object, they elastically rebound and transfer momentum. We measure pressure in units of Pascals (Pa) which are equal to one Newton per square meter, and it is calculated as we see in Equation 2 by the force of the collisions divided by the area over which they come into contact.
![]()
We feel a constant air pressure on our bodies as particles in the air run into us. At sea level, the air pressure is known as 1 atmosphere (1 atm) of pressure, which is equal to 101,325 Pa. This air pressure includes the weight of all the air above you in our atmosphere pushing down on you. If you go to a higher altitude, the air pressure decreases because the column of air above your head gets smaller. Similarly, if you dive under water (or another fluid), the deeper you go, the more water pressure you have pushing down on you (the more fluid is located above your head). To determine the pressure ![]() at some height
at some height ![]() above or below the water, you would use the following equation.
above or below the water, you would use the following equation.
![]()
In the above equation, ![]() is the new pressure at some height
is the new pressure at some height ![]() ,
, ![]() is a known pressure at a height defined as zero,
is a known pressure at a height defined as zero, ![]() is the local gravitational constant, and
is the local gravitational constant, and ![]() is the density of the fluid producing the pressure. If you take
is the density of the fluid producing the pressure. If you take ![]() to be air pressure at sea level,
to be air pressure at sea level, ![]() gets lower as you go up (use
gets lower as you go up (use ![]() = -9.81 m/s
= -9.81 m/s![]() ) and
) and ![]() gets higher if you go down or under a fluid. Remember to draw a picture of the situation you are dealing with and determine ahead of time if your new pressure
gets higher if you go down or under a fluid. Remember to draw a picture of the situation you are dealing with and determine ahead of time if your new pressure ![]() should be higher or lower than your original pressure
should be higher or lower than your original pressure ![]() to make sure your answer makes sense.
to make sure your answer makes sense.
Section 14.3: Pascal’s Principle
Textbook Section 14.3: Pascal’s Principle and Hydraulics
Pascal’s Principle states that when you change the pressure on one part of an enclosed fluid, the change in pressure is applied to all parts of the enclosed fluid equally, as well as the walls of the container. Because pressure is equal to force over area, if the same pressure is applied on two different areas, two different forces are applied, as we see in the following equation.
![]()
This is the principle behind the hydraulic lift. Applying a small force on a small area connected by a fluid to a large area results in a large force acting on the large area.
Section 14.4: Buoyancy
Textbook Section 14.4: Archimede’s Principle and Buoyancy
We saw that with air pressure, the air above you pushes down on you. However, the air to the side and below you (if you’re suspended in air somehow) also push on you in other directions. The force of a fluid pushing on you opposite the force of gravity is called the buoyancy force. Buoyancy is the force that pushes back when you try to push a balloon under the water, and the reason why you float in a pool of water. The buoyancy force ![]() is equal to the weight of the displaced fluid. If you completely submerge an object in a fluid, it displaces an amount of fluid equal to its volume. However, if an object is floating in a fluid but not completely submerged, it instead displaces a smaller volume of fluid. The volume of fluid displaced is equal to the volume of the object that is under the surface of the fluid. When solving buoyancy problems, draw yourself a free body diagram for the object in question and make sure to keep track of the different densities, masses, and volumes correctly.
is equal to the weight of the displaced fluid. If you completely submerge an object in a fluid, it displaces an amount of fluid equal to its volume. However, if an object is floating in a fluid but not completely submerged, it instead displaces a smaller volume of fluid. The volume of fluid displaced is equal to the volume of the object that is under the surface of the fluid. When solving buoyancy problems, draw yourself a free body diagram for the object in question and make sure to keep track of the different densities, masses, and volumes correctly.
Section 14.5: Fluid Dynamics
Textbook Section 14.5: Fluid Dynamics
Textbook Section 14.6: Bernoulli’s Equation
Fluid dynamics refers to fluids that are moving in some fashion. For this introduction to fluid mechanics, we will only consider ideal fluids (no internal friction, know as viscosity, no turbulent motion, and an incompressible fluid). A fluid moving through a pipe that cannot be compressed means that the same amount of fluid must go past a certain point in a certain amount of time (say, every second). This does not mean that the fluid always has the same velocity — if the pipe suddenly became far more narrow, a fluid moving at the same velocity everywhere would only move part of the total amount past a certain point per second. This principle, known as the continuity equation (see equation below) actually means that a fluid passing through a more compressed space must move faster in that smaller space to transport the same amount of fluid in a second.
![]()
In the equation above, the velocity ![]() of the fluid passing through a pipe of cross-sectional area
of the fluid passing through a pipe of cross-sectional area ![]() changes to
changes to ![]() as the pipe changes to a cross-sectional area of
as the pipe changes to a cross-sectional area of ![]() .
.
When you have a change in height of the tube, the pressure can change as well as the velocity and energy of the fluid. Bernoulli’s Equation (equation below) is similar to a conservation of energy equation for fluids, describing how these variables are related.
![]()
In Class Group Problem 14.1:
Airplane windows are made up of three layers with air gaps in between — an outer glass layer, a middle glass layer with a small hole in it, and an inner plastic layer which mostly serves to keep passengers from damaging the middle layer.
When flying at a normal cruising altitude of 30,000 feet, the pressure outside the airplane has dropped from 14.7 PSI (lbs/in![]() ) at sea level to 4.30 PSI. The drastically decreased air pressure would make it impossible for humans to breathe in enough oxygen to stay conscious, so the airplane cabin is pressurized to the equivalent of being at 7,000 feet (11 PSI).
) at sea level to 4.30 PSI. The drastically decreased air pressure would make it impossible for humans to breathe in enough oxygen to stay conscious, so the airplane cabin is pressurized to the equivalent of being at 7,000 feet (11 PSI).
Find the pressure inside and outside the plane in Pascals at a typical cruising altitude.
The hole in the middle of the glass pane of the windows allows the pressure to equalize between the plastic and glass layers so that the outer glass window supports most of the force that results due to the imbalance in pressures. The hole also keeps moisture from forming between the panes. If the average surface area of an airplane window is 115 in![]() , what net force is exerted on the window, and which way does this force point (in or out of the plane)?
, what net force is exerted on the window, and which way does this force point (in or out of the plane)?
If the outer window breaks under the force, the inner glass layer can support the pressure difference until the plane is able to descend to a safer altitude. The small hole, which is now a leak, is easily compensated for by the pressure system of the plane.
The difference in air pressure between the ground and cabin when flying causes the same kind of force (although not as large) on your inner ear, causing pain until you can cause your ears to “pop” by draining fluid out the Eustachian tube into your nose and equalizing the pressure inside your head with the cabin pressure. Small children (and people flying with head colds) have trouble doing this, which is the cause of most of the crying kids on planes.
If this happens to you, do not attempt to fix the problem by blowing your nose! This can cause your eardrums to rupture, leaving you with much more serious problems. Instead, close your mouth, hold your nose, and turn your head as far as you can to the side while swallowing. Continue this back and forth until your ears pop naturally.
In Class Group Problem 14.2:
A swimmer in a pool (![]() = 1.0 g/cm
= 1.0 g/cm![]() ) dives from just above the surface (at sea level) to 3.5 m below the surface of the water. What is the pressure on the swimmer in atm below the surface?
) dives from just above the surface (at sea level) to 3.5 m below the surface of the water. What is the pressure on the swimmer in atm below the surface?
In Class Group Problem 14.3:
What force do you need to apply to area 2 of a hydraulic lift with areas ![]() = 0.35 m
= 0.35 m![]() and
and ![]() = 0.0067 m
= 0.0067 m![]() if you want to lift your 2,000 lb car a total of 2.0 meters in the air?
if you want to lift your 2,000 lb car a total of 2.0 meters in the air?
In Class Group Problem 14.4:
The manometer below is filled with water. If the right side is open to air pressure, ![]() = 3.5 cm, and
= 3.5 cm, and ![]() = 0.75 cm, what is the pressure
= 0.75 cm, what is the pressure ![]() ?
?
The density of water is 1,000 kg/m![]() at room temperature. The density of mercury is 13.56 g/cm
at room temperature. The density of mercury is 13.56 g/cm![]() . You want to make a barometer capable of measuring atmospheric pressure at sea level. How long does the tube need to be if you make it out of water? How about if you make it out of mercury?
. You want to make a barometer capable of measuring atmospheric pressure at sea level. How long does the tube need to be if you make it out of water? How about if you make it out of mercury?
In Class Group Problem 14.5:
You drop a spherical, latex balloon (![]() = 5.0 g, radius
= 5.0 g, radius ![]() = 7.0 cm) filled with air from a height of 3.0 m. How long does it take to reach the ground if the density of air is
= 7.0 cm) filled with air from a height of 3.0 m. How long does it take to reach the ground if the density of air is ![]() = 1.225 kg/m
= 1.225 kg/m![]() ?
?
In Class Group Problem 14.6:
You have been hired to lift a statue out of the ocean. The statue has a mass of 500 kg and is made entirely out of silver (10.49 g/cm![]() ). The density of seawater is 1030 kg/m
). The density of seawater is 1030 kg/m![]() . The statue is lifted at a constant velocity.
. The statue is lifted at a constant velocity.
What is the tension in the cable supporting the statue when the statue is completely under the water?
What is the tension in the cable when the statue is completely above the water and still moving at a constant velocity? Ignore the buoyancy due to air.
In Class Group Problem 14.7:
At the end of the movie Titanic, Rose lies on a piece of furniture, floating in the ocean, and Jack drowns. A common objection posed to this scene is that there’s room on the furniture for Jack as well, so why didn’t she let him get on it with her?
Let’s assume that the piece of furniture has an area of 1.5 m![]() , a thickness of 5 cm, and is made of pine (
, a thickness of 5 cm, and is made of pine (![]() = 350 kg/m
= 350 kg/m![]() ). Assuming Rose has a mass of 46 kg and Jack has a mass of 58 kg, could they have both managed to stay afloat on the raft together?
). Assuming Rose has a mass of 46 kg and Jack has a mass of 58 kg, could they have both managed to stay afloat on the raft together?
In Class Group Problem 14.8:
In Class Group Problem 14.9:
In Class Group Problem 14.10:
You have been hired by Nintendo to do the physics for a new Mario Brothers level. This underwater level includes large stone blocks falling on Mario from above. The blocks begin to fall when Mario first steps directly beneath them, and are cubic with each side 1.70 m long in Mario’s world. The blocks will fall from a height of 3.50 m (at the base of the block) above the ground, and Mario is 1.50 m tall. If the density of the blocks is 2,350 kg/m![]() and the density of water is 1,000 kg/m
and the density of water is 1,000 kg/m![]() , what is the minimum speed at which Mario must be running to avoid getting hit in the head by a block? Ignore drag.
, what is the minimum speed at which Mario must be running to avoid getting hit in the head by a block? Ignore drag.
In Class Group Problem 14.11:
Gaseous helium has a density of ![]() = 0.1786 kg/m
= 0.1786 kg/m![]() and air has a density of
and air has a density of ![]() = 1.225 kg/m
= 1.225 kg/m![]() . You have decided to recreate the balloon scene from “Up” with yourself (62 kg), your lawn chair (3.0 kg), and a bunch of helium-filled balloons 12 inches in diameter.
. You have decided to recreate the balloon scene from “Up” with yourself (62 kg), your lawn chair (3.0 kg), and a bunch of helium-filled balloons 12 inches in diameter.
How many balloons do you need to attach to your lawn chair to keep yourself and the lawn chair at a stable altitude without sinking or rising? You have already determined the balloons each have an un-inflated mass of 4.0 g.
In Class Group Problem 14.12:
At your next family gathering at the lake, you want to fool your cousins into thinking you can walk on water. You design a piece of wood so that when you, a 50 kg person, walk on it, the wood is entirely submerged but you are entirely out of the water (just the bottom of your feet get wet). The wood is 2.0 m long and wide and 37 cm thick. What density of wood do you need to use for your trick to work?
Practice Exam Question 14.1:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
You have a square plastic box made of acrylic (density ![]() = 1.18 g/cm
= 1.18 g/cm![]() ) with a side length of 18 cm and a side thickness of 1.0 cm. The box is filled with air (density
) with a side length of 18 cm and a side thickness of 1.0 cm. The box is filled with air (density ![]() = 1.225 kg/m
= 1.225 kg/m![]() ). How many lead pellets (8 g each, density
). How many lead pellets (8 g each, density ![]() = 11.34 g/cm
= 11.34 g/cm![]() ) do you need to add to the box before it will sink in water (density
) do you need to add to the box before it will sink in water (density ![]() = 1000 kg/m
= 1000 kg/m![]() )?
)?
Practice Exam Question 14.2:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
Alvin is a manned deep-ocean submarine run by Woods Hole Oceanographic Institute in Massachusetts. It can dive up to 4,500 m. It is pressurized inside to 1.00 atm. What is the net force on its circular 0.51 m diameter plug hatch while sitting at a depth of 4,200 m below the surface of the Pacific Ocean in the Marianas Trench?
![]() kg/m
kg/m![]()
Practice Exam Question 14.3:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
You are designing a spherical submersible vessel that can remain at a particular depth underwater indefinitely without rising to the top or sinking to the bottom. The vessel is made of aluminum and the inside is filled with air. If the radius of the vessel is 2.60 m, and aluminum costs $0.91/lb, how much will it cost you to buy the materials for the vessel?
![]() g/cm
g/cm![]()
Practice Exam Question 14.4:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
A hollow cube of copper floats in a pool of petrol. The inside of the cube (which has sides of length 21.0 cm and a side thickness of 0.200 cm) is filled with a vacuum and water. What percentage of the hollow volume of the cube is filled with water if the cube floats without sinking when entirely surrounded by petrol?
Practice Exam Question 14.5:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
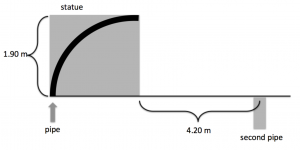
A new hotel in Las Vegas has hired you to design a water feature for them. The water enters the bottom of a pipe (with some initial velocity) as shown, travels up to the top of a 1.90 m statue, and leaves the pipe at some new horizontal velocity. The water needs to land in another pipe leading to a fish tank down below, 4.20 horizontal meters from the pipe the water left. How fast does the water need to be moving at the bottom of the statue for it to land in the second pipe? Ignore air resistance. The pressure and density of the water remain constant while in the pipe, and the radius of the pipe changing by some amount you don’t need to know or calculate.
Practice Exam Question 14.6:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
A plastic balloon is filled with air. The air portion of the ballon has a radius of 11.00 cm; the plastic portion of the balloon extends from 11.00 cm to 11.09 cm.
The balloon rests on a scale in a room that has been completely evacuated of air. What weight (in N) does the scale register for the balloon filled with air?
The room is filled with air. What does the scale read now (in N)? (Hint: think about what force the air might be exerting on the balloon).
Practice Exam Question 14.7:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
The human eardrum is a membrane with a surface area of 4.8 ![]() 10
10![]() m
m![]() , and it separates the inside of your ear (at atmospheric pressure) from the outside pressure on your ear. The eardrum can withstand a net force of 5.1 N before rupturing. How deep can someone dive below the surface of a lake before rupturing their eardrum? The surface of the lake is at atmospheric pressure.
, and it separates the inside of your ear (at atmospheric pressure) from the outside pressure on your ear. The eardrum can withstand a net force of 5.1 N before rupturing. How deep can someone dive below the surface of a lake before rupturing their eardrum? The surface of the lake is at atmospheric pressure.
A material with a fixed shape and volume. The atoms/molecules in the substance have strong molecular bonds holding them in place.
A material with fixed volume (incompressible) but no fixed shape. It can flow to take the shape of the bottom of it's container.
A material with no bonds between it's atoms/molecules. It can change shape and volume to take the shape of it's container.
Mass over volume.
Defined as force over area, and caused by particles colliding with surfaces of an object.
Pressure caused by air pushing on an object. Decreases as height in the atmosphere increases.
The force applied to an object by a fluid it is in contact with. The buoyant force is equal to the weight (mass times gravity) of the fluid displaced by the object.
A fluid (gas or liquid) with no internal friction or collision between particles.

