Chapter 13: Gravitation

Adria Updike

12 Chapter 13: Gravitation

Textbook Section 13.1: Introduction to Gravitation

Yes, we’re skipping Chapter 12 in the textbook, so I’m keeping notation the same here.

Section 13.1: Newton’s Universal Law of Gravitation

Textbook Section 13.1: Newton’s Law of University Gravitation

I know what you’re thinking – didn’t we do this back in Chapter 5? Well, not really. The law of gravity we’ve been using so far, $F_g = mg$ , assumes you’re on the surface of the Earth. That little $g$ , the gravitational constant, is only equal to $-9.81$ m/s $^2$ on the surface of the Earth, and only some parts of the Earth’s surface at that. Now we’re going to look at the full form of the equation, known as Newton’s Law of Gravity, which works everywhere in the universe, including on the surface of the Earth.

$F_G = \frac{G m_1 m_2}{R^2}$

In the above equation, $G$ is the gravitational constant (equal to about $6.67 \times 10^{-11}$ N m²/kg²), $m_1$ and $m_2$ are the masses of two objects attracting each other gravitationally, and $R^2$ is the straight-line distance between the centers of mass of the two objects.

Section 13.2: The Origin of g

Textbook Section 13.2: Gravitation Near the Earth’s Surface

So if that’s the real law of gravity, where did little $g$ , our gravitational acceleration, come from? Remember we said that $F_g = mg$ applies on the Earth’s surface, and $F_G$ above applies everywhere. That means that on the Earth’s surface, $F_G = F_g$ .

$F_G = F_g = \frac{G m_1 m_2}{R^2} = mg$

Since the $m$ in $F_g = mg$ is the thing that isn’t the Earth (like you, or a ball, or whatever you’re talking about sitting on the Earth) the other $m$ must be the Earth. So that means:

$g = \frac{G m_{Earth}}{R_{Earth}^2}$

Section 13.3: Gravitational Potential Energy

Textbook Section 13.3: Gravitational Potential Energy and Total Energy

We derived $PE_g$ from the gravitational force near the Earth’s surface. When we’re no longer close to the surface of the Earth, we need a new form for the potential energy due to Earth’s gravity. We’re going to call this new form of the gravitational potential energy $U$ .

$U = -\frac{G m_1 m_2}{R}$

Now $U$ is the gravitational potential energy between any two objects where one of them isn’t sitting on the surface of the Earth (or very close to it), at least not at every point in the problem.

Why the negative sign? It’s simply how we define it. Let’s look at how $U$ would play into a conservation of energy equation for an object in space falling to the surface of the Earth.

$\frac{1}{2} m v_i^2 - G \frac{m_{Earth} m_{object}}{r_i} = \frac{1}{2} m v_f^2 - G \frac{m_{Earth} m_{object}}{r_f}$

It works out just like we saw for normal conservation of energy for a falling object – as it gets closer to the Earth, it moves faster.

Section 13.4: Orbital and Escape Velocities

Textbook Section 13.4: Satellite Orbits and Energy

But not everything falls to Earth. We have thousands of satellites, man-made and otherwise (like the Moon) in stable orbits around the Earth. How does that work? It turns out that every distance away from the Earth has associated with it a particular velocity called the orbital velocity. If you move at that velocity, you can continually circle the Earth at a constant distance without ever falling into the Earth. Imagine it like a marble in a bowl. If you swing the bowl around at a certain velocity, the marble will make a circle around the top part of the bowl and won’t fall in. It’s the same general idea.

$v_{orbit} = \sqrt{\frac{G M_{Earth}}{r}}$

The orbital velocity above is a function of the mass of the object you’re orbiting (in this case, the Earth, but any object mass works in it’s place) and how far you are from the center of mass of the object you’re orbiting.

$T = 2 \pi \sqrt{\frac{r^3}{G M_{Earth}}$

Similarly, the period $T$ (in seconds) of the orbit is how long it takes to make a full circular orbit of the Earth at a particular distance.

Finally, the escape velocity $v_{esc}$ is how fast you need to be moving in order to have enough energy to escape Earth’s gravitational pull. When launching satellites into space, they need to be moving at least this fast to get away from the surface and go into space, or even into orbit.

$v_{esc} = \sqrt{\frac{2 G M_{Earth}}{r}$

In Class Group Problem 13.1:

Astrologers, who attempt to predict the future based on the positions of celestial objects such as planets and stars, claim that the positions of the objects relative to you determine the course of your life.

Find the gravitational force of the planet Jupiter ( $M_J = 1.9 \times 10^{27} kg$ ) on you, a 60 kg person on Earth, when Jupiter is at its closest approach to Earth (391 million miles).

Find the gravitational force of a passing bus ( $M_B = 10,000$ lbs) passing by you on the street at a distance of 1 meter.

Make a case for why astrologers are or are not correct based on your above calculations.

In Class Group Problem 13.2:

How far can you move above the surface of the Earth before $g$ can no longer be used to calculate your potential energy relative to the surface? Assume $g$ is no longer valid if the value changes by more than 5 $\%$ . The mass of the Earth is $5.97 \times 10^{24}$ kg, and the radius of the Earth is 6,378 km.

In Class Group Problem 13.3:

You, an almighty being of some sort, drop a planet next to a star with the intention of putting it in orbit around the star. However, you forget to give it some initial velocity perpendicular to the star, so the planet, gravitationally attracted to the star, begins moving in a straight line towards the star. A few hours later, you notice your mistake when the star is halfway between its initial location and the star and now rapidly approaching the star. How fast is the planet moving at this point?

Should you use kinematics to figure this out? Why or why not?

How can you solve this problem if you don’t use kinematics?

Solve this problem to find an equation for the final velocity of the planet $v_f$ of mass $m_p$ originally placed some distance $d$ from the star of mass $m_s$ .

In Class Group Problem 13.4:

You have been exploring the Martian moon of Deimos ( $m_{Deimos} = 1.48 \times 10^{15}$ kg) and are preparing to leave. At what minimum velocity do you need to leave the surface to escape the gravity of Deimos? Assume Deimos is spherical (it’s not) with a radius of 6,200 m (it’s small!) and your spaceship has a mass of 12,000 kg.

In Class Group Problem 13.5:

SpaceX has hired you as a consultant to help launch its Dragon capsule (at a weight of 9,259 lbs) into orbit to reach the International Space Station (ISS). The ISS orbits above the Earth at a distance of 249 miles above the surface. You want to launch the Dragon so that it comes to a stop due to the gravitational pull of the Earth just as it reaches the ISS. What initial velocity do you need to give the Dragon capsule at lift-off (assuming the rockets do nothing after you leave the ground)? Hint: you’re smart enough to launch the satellite to where the ISS will be when it reaches the rendezvous point, so it can move in a straight line instead of a curved path.

In Class Group Problem 13.6:

What orbital velocity must the ISS attain in order to stay in a circular orbit above the Earth at a constant distance (249 miles) above the surface? The ISS has a mass of 925,000 lbs.

In Class Group Problem 13.7:

NASA wants to put its new satellite into a circular orbit of the Moon ( $m_{Moon} = 7.34 \times 10^{22}$ kg, $r_{Moon} = 1,737$ km). It costs NASA about $10,000 per pound of material to launch, so they don’t want to put too much memory storage (and therefore weight) on the satellite itself. Instead, they have it communicate with a ground station by uploading all the information it took every 6 hours as it passes over the ground station located at the Moon’s north pole. If the satellite has to pass over the pole every 6 hours, how far above the surface of the Moon is the satellite located?

In Class Group Problem 13.8:

You are reading a magazine about pulsars. A few years ago, a satellite in orbit around the Earth detected x-rays coming from sources in outer space. The x-rays detected from one source, called Cygnus X-3, had an intensity which changed over a period of 4.8 hours. This type of astronomical object emitting periodic signals is called a pulsar. One popular theory holds that the pulsar is a normal star (similar to our Sun) which is in orbit around a much more massive neutron star. The period of the x-ray signal is then the period of the orbit. In this theory, the distance between the normal star and the neutron star is approximately the same as the distance between the Earth and the Sun. You realize that if this theory is correct, you can determine how much more massive the neutron star is than our Sun. Perform this calculation if the Earth has an average distance from the Sun of 93 million miles and our Sun has a mass of $6 \times 10^{30}$ kg.

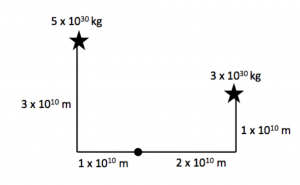
Practice Exam Question 13.1:

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

What is the net gravitational force (magnitude and direction) on the satellite of mass 2,000 kg (round circle below)?

License

Icon for the Creative Commons Attribution 4.0 International License