Chapter 15: Thermodynamics

Adria Updike

14 Chapter 15: Thermodynamics

This is the last unit of PHYS 201, but starts on the second volume of the textbook, and chapter numbering starts over. Since we don’t cover everything in the thermodynamics unit, we’ll combine some of the more useful parts of the four chapters on thermodynamics here into one section.

Section 15.1: Temperature Scales

Textbook Section 1.1: Temperature and Thermal Equilibrium

Textbook Section 1.2: Thermometers and Temperature Scales

Heat is defined as the energy transferred from one system to another due to a temperature difference in the systems. Heat always flows from the hot system from the cold system; it never flows in the other direction.

Temperature is a measure of the kinetic energy of the particles making up a system. Thermodynamics refers to heat exchange between systems. A thermometer is an instrument that measures temperature by the way certain materials respond to changes in heat content. When systems are in thermal equilibrium with each other, the systems have identical temperatures and no more heat is being exchanged between the systems. An insulator attempts to prevent the transfer of heat from a hot system (say, a coffee mug) to a colder one (the air your classroom).

There are three main temperature scales you will run into. Each scale picks two set points (a certain fluid at a certain density and pressure, thus a certain temperature) and determines the size of the scale steps between and around these points. The Fahrenheit scale uses the freezing point of water (32 $^{\circ}$ F on the Fahrenheit scale) and boiling point of water (212 $^{\circ}$ F on the Fahrenheit scale) to define temperature. There are 180 $^{\circ}$ F between these two points.

The Celsius scale also uses the freezing and boiling points of water, but on the Celsius scale, these points occur at 0 $^{\circ}$ C and 100 $^{\circ}$ C. There are only 100 $^{\circ}$ C steps between these two points. Therefore, a change of one degree C is \emph{not} equivalent to a change of one degree C.

To convert back and forth between these systems, use the conversions below.

$T_f = \frac{9}{5} T_c + 32$

$T_c = \frac{5}{9} \left( T_f - 32 \right)$

Gas thermometers are the most accurate thermometers, but are not commonly used because they can take up entire rooms. In a gas thermometer, as the temperature of the fluid enclosed increases, so does the temperature. Every different type of fluid changes differently with pressure. When graphed (temperature vs pressure), all the lines appeared to be converging at a single point in the negative part of the Celsius temperature range. This temperature that all fluids can theoretically reach (but we’ve never quite gottenabsolute zero any of them all the way there) is called absolute zero, and is the basis of the third temperature scale, the Kelvin scale.

The Kelvin scale starts at absolute zero (basically no motion of particles at all in anything) and goes up from there. It hits the freezing point of water at 273.15 K (note we don’t use “degrees” when talking about Kelvin), so the conversion from Celsius to Kelvin is

$T_k = T_c + 273.15.$

Section 15.2: Thermal Expansion

Textbook Section 1.3: Thermal Expansion

Most materials expand when energy is added in the form of heat. This makes sense in terms of how we have talked about energy; giving energy to a system makes the particles more active, they move around more with higher velocities, collide with themselves and the walls of the container more often, applying pressure to the container and expanding the overall material.

Linear thermal expansion refers the expansion that occurs in a single direction along a material. The equation for linear expansion is given as

$\Delta L = \alpha \, L_0 \, \Delta T$

where $L_0$ is the original length of the material, $\Delta L$ is the change in length (not the new length!), $\Delta T$ is the change in the temperature of the material (in either Celsius or Kelvin because they have the same step sizes), and $\alpha$ is the coefficient of linear expansion, a constant that differs for every material. We can also define a volumetric thermal expansion equation,

$\Delta V = \beta \, V_0 \,\Delta T$

relying on the original volume, change in volume, change in temperature, and a coefficient of volumetric expansion $\beta$ .

Section 15.3: The Ideal Gas Law

Textbook Section 2.1: Molecular Model of an Idea Gas

Textbook Section 2.2: Pressure, Temperature, and RMS Speed

We usually consider an ideal gas in physics to simplify our calculations, and it’s not a bad assumption for most systems. An ideal gas has a large number of particles that are non-interacting; we do not consider particle collisions when determining pressure.

The ideal gas law, which you may have encountered previously in chemistry, states the relationship between the gas pressure $p$ , the volume of the gas $V$ , the number of atoms or molecules in the gas $N$ , the temperature $T$ (in Kelvin), and a constant $k$ called Boltzmann’s constant.

$pV = NkT$

The average kinetic energy of a molecule in a gas is given by

$KE_{av} = \frac{1}{2} m v_{av}^2 = \frac{3}{2} k T$

We talk about the average velocity of a molecule because any groups of molecules or atoms in a gas have a velocity distribution called the Maxwell-Boltzmann velocity distribution. This distribution tapers off fasters on the lower end of possible velocities, has a most probable velocity, an average velocity (also called the root-mean-squared velocity, or $v_{rms}$ ), and has a longer tail towards higher velocities. This velocity distribution gives you the probability of finding your particle at many possible velocities.

Section 15.4: Thermodynamics

Textbook Section 1.4: Heat Transfer, Specific Heat, and Calorimetry

In the previous chapter, we defined heat as energy transferred between systems or objects due to the temperature difference between the objects, and pointed out that heat is only transferred from hot to cold objects, not the other way around.

Besides energy measured in Joules, we have other units of heat we can work with. A calorie is a unit of heat energy, and is the amount of energy required to raise the temperature of 1 g of water from 14.5 $^{\circ}$ C to 15.5 $^{\circ}$ C. One calorie is equivalent to 4.186 J. But if you look at calories on your packages of food, it’s not measured in real calories. Food energy contact is given in units of kilocalories (Cal in the US, kcal in Europe), where 1,000 cal = 1 Cal = 1 kcal = 4,186 J.

A BTU (British Thermal Unit is the amount of energy required to raise the temperature of 1 lb of water from 63 $^{\circ}$ F to 64 $^{\circ}$ F. 1 BTU = 1,055 J.

The heat transfer equation tells us how a specific material reacts to energy input in the form of heat.

$Q = m\, c\, \Delta T$

In the equation above, $Q$ is the amount of heat energy entering or leaving a system, $m$ is the mass of the system, $c$ is the specific heat of the substance (a constant for each material defining how it responds to heat increase) and $\Delta T$ is the resulting temperature change (in units or either Celsius or Kelvin). $c$ has units of J/(kg K) or J/(kg $^{\circ}$ C).

Both $m$ and $c$ are positive quantities, but the material can either gain energy (get hotter) or lose energy (get colder) and as a result $Q$ can be either positive or negative. We consider our systems to be isolated systems, or in other words, systems that do not exchange matter or energy with any outside system (as opposed to closed systems, which only exchange energy, and open systems, which exchange both matter and energy with outside systems).

Energy is a conserved quantity. Heat energy lost by one part of the system will always be gained by another part of the system. When we add up all the $Q$ values associated with all the systems in contact, the total $Q$ gained or lost (sum of $Q's$ ) must be equal to zero.

Calorimetry is a way of measuring heat. When a sufficient quantity of heat is added to a system, the system is capable of undergoing a phase change from one phase (solid, liquid, or gas) to another phase. The heat exchange associated with a phase change is a separate interaction from the heat exchange used to heat up or cool down a system, and is given by

$Q = \pm m\, L_f$

where $m$ is the mass of material undergoing a phase change, and $L_f$ is known as the latent heat of fusion (also can be $L_v$ , the latent heat of vaporization). Latent heats are the amount of heat per kg of material that it takes for that mass of material to undergo the complete phase change. They are constants that must be measured for different materials at different phase changes.

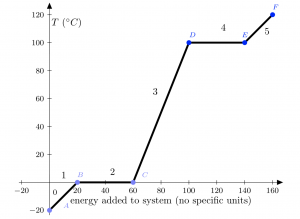
Consider the above diagram. This diagram charts the approximate progress of a 10 kg block of ice at -20 $^{\circ}$ as heat is gradually added to the block in a systematic manner (say, putting it in a pot on the stove).

When you begin to add heat, what will happen to the ice? Will it heat up? Will it melt? Will it evaporate? The phase change temperatures can help us here. We know that water changes phases at 0 $^{\circ}$ C (goes from solid to liquid) and 100 $^{\circ}$ C (goes from liquid to gas). These phase transitions happen only at these temperatures, and no other! If our block of ice is not at one of these temperatures (and it isn’t, at -20 $^{\circ}$ C), then it cannot immediately change phase. First, it must either heat up or cool down to reach the next phase change temperature.

As heat is added to the block of ice, it heats up from -20 $^{\circ}$ C to 0 $^{\circ}$ C. This is step 1 on the diagram, between points $A$ and $B$ . The block stops heating up at this point because we have reached a phase change temperature. At the moment, the entire block is at 0 $^{\circ}$ C and is in the ice (solid) phase. This is equation $Q_1$ , where $Q_1 = m_{ice} c_{ice} \Delta T_{-20 C\, to\, 0 C}$ .

What happens next? As we continue to add heat to the block of ice, the temperature does not increase further. Since we have reached a phase change temperature, any additional heat added will go into melting the ice to its liquid form (water). No additional energy will heat the water from 0 $^{\circ}$ C until the entire block of ice has completely changed phase. This is section 2 of the diagram, between points $B$ and $C$ . Note the temperature remains constant during this time as the ice changes phase to water. The equation we use here is for phase change, not energy addition, so $Q_2 = + m_{ice} \, L_f$ . This is a positive addition because the ice is heating up (energy is being added) and we use the latent heat of fusion $L_f$ for the ice/liquid transition (in either direction, ice to liquid or liquid to ice).

After all of the ice has transformed into water, any additional heat added will go into heating up the water until the water hits the next phase transition temperature (liquid to gas at 100 $^{\circ}$ C). This phase is section 3 of the diagram, between points $C$ and $D$ . This is another addition of energy equation, so our third $Q$ value will be $Q_3 = m_{ice} c_{water} \Delta T_{0 C \, to \,100 C}$ . Note that we are still referring to the mass as $m_{ice}$ . We could easily call this $m_{water}$ instead, since the ice has now transformed into water, but we will continue calling it the mass of the ice to avoid confusion of variables, especially since $c_{ice}$ and $c_{water}$ have different values.

When all of the water is at 100 $^{\circ}$ C, the added heat now goes into changing the phase of the water for a second time, from liquid water to gas phase. This is the fourth section of the graph, between points $D$ and $E$ . Note again that the temperature of the entire system remains constant during the phase change. Again, we have a phase change $Q_4 = m_{ice} L_v$ , where $L_v$ is the latent heat of vaporization.

After all of the water has turned into water vapor (gas), any additional energy added to the system simply goes into heating up the gas further. Our final step on the diagram, step 5 from points $E$ to $F$ , will be $Q_5 = m_{ice} c_{vapor} \Delta T_{100C \, to 120C}$ . We arbitrarily stop this process at 120 $^{\circ}$ C; it could easily go much higher.

Go back over all those steps and make sure you know what’s happening to our original block of ice at each phase. Is it heating up? Changing phase? What kind of heat equation do we need for each transition?

Finally, looking at the sum of our $Q's$ , we can write a full equation for the amount of heat added to this system.

$Q_{total} = Q_1 + Q_2 + Q_3 + Q_4 + Q_5$

$Q_{total} = m_{ice} c_{ice} \Delta T_{-20 C\, to\, 0 C} + m_{ice} \, L_f + m_{ice} c_{water} \Delta T_{0 C \, to \,100 C} + m_{ice} L_v + m_{ice} c_{vapor} \Delta T_{100C \, to 120C}$

The equation above is the sum of all the heat added to the block of ice. Does it equal zero? No. Should it? No. It’s only equal to zero if we then subtract all the heat given to the ice by the stove.

In Class Group Problem 15.1:

The temperature of the surface of our Sun is 5,788 K. What is this in degrees Fahrenheit?

In Class Group Problem 15.2:

The surface of Pluto is -223 $^{\circ}$ C on average. What is this in Kelvin?

In Class Group Problem 15.3:

You have a 3.0 kg bar of gold at room temperature (20 $^{\circ}$ C). What is the volume of this gold bar if you heat it up to 50 $^{\circ}$ C?

In Class Group Problem 15.4:

The Mt. Hope Bridge is 1,867 m long on the coldest day and is made out of steel ( $\alpha_{steel}$ = 1.2 $\times 10^{-5}$ K $^{-1}$ ). The lowest temperature recorded in Bristol was –17 $^{\circ}$ F in 1934, and the highest temperature was 104 $^{\circ}$ F in 1976. Find $\Delta L$ of the bridge between these extreme temperatures.

In Class Group Problem 15.5:

When an object with a hole in it is heated and expands, the hole expands at the same rate as the object. At 20 $^{\circ}$ C, an aluminum ring has an inner diameter of 4.5000 cm, and a brass rod has a diameter of 4.5500 cm. Keeping the brass rod at 20 $^{\circ}$ C, to what temperature do you need to heat the ring so that it just barely fits over the brass rod? The coefficient of linear expansion for aluminum is $\alpha = 2.40 \times 10^{-5}/^{\circ}$ C.

In Class Group Problem 15.6:

A steel sphere sits on top of an aluminum ring. The steel sphere ( $\alpha = 1.10 \times 10^{-5}/^{\circ}$ C) has a diameter of 4.0000 cm at 0 $^{\circ}$ C. The aluminum ring ( $\alpha = 2.40 \times 10^{-5}/^{\circ}$ C) has an inside diameter of 3.9940 cm at 0 $^{\circ}$ C. Find the lowest temperature at which the sphere will be able to fall through the ring.

In Class Group Problem 15.7:

Measure how high you can jump. Assuming your muscles are 25\% efficient (25\% of the energy spent went into moving you up into the air and back down again), how much energy did you burn in that jump? Use conservation of energy to answer this.

A “fun pack” of M\&Ms has 230 kcal. How many times would you have to jump in order to burn off a small package of M\&Ms?

When jumping rope at an average speed, you make about 70 jumps per minute. How long would you need to spend jumping rope in order to burn off a fun pack of M\&Ms?

In Class Group Problem 15.8:

A 15.0 kg piece of aluminum (with $c_{Al}$ = 900 J/kg $^{\circ}$ C) is warmed so that its temperature changes by 7.00 $^{\circ}$ C. How much heat was transferred to the aluminum?

In Class Group Problem 15.9:

You put a 2.5 kg copper ( $c_{Cu}$ = 387 J/kg $^{\circ}$ C) pot containing 1.2 kg of water ( $c_{H_2O}$ = 4186 J/kg $^{\circ}$ C) on the stove, which has a wattage of 5,000 W (the stove produces 5,000 J/s). How long (in minutes) does it take the pot and water to reach 100 $^{\circ}$ C if they start at 20 $^{\circ}$ C? Assume all the energy the stove produces goes into the pot and water system.

In Class Group Problem 15.10:

A 3.0 g lead bullet is traveling at a speed of 240 m/s when it embeds in a wood post. If we assume that half the resultant heat energy generated remains with the bullet, what is the increase in temperature of the embedded bullet? $c_{lead}$ = 0.0305 kcal/kg $^{\circ}$ C, 1 kcal = 4186 J).

Hint: what is the overall change in energy of the bullet?

In Class Group Problem 15.11:

A 0.20 kg aluminum plate, initially at 20 $^{\circ}$ C, slides down a 15 m long surface included at an 30 $^{\circ}$ angle to the horizontal. The force of kinetic friction exactly balances the component of gravity down the plane so that the plate, once moving, glides down at a constant velocity. If 90\% of the mechanical energy (sum of potential and kinetic) of the system is absorbed by the aluminum, what is the temperature increase at the bottom of the incline? $c_{Al}$ = 900 J/kg $^{\circ}$ C

In Class Group Problem 15.12:

A hot (70 $^{\circ}$ C) lump of metal has a mass of 250 g and a specific heat of 0.25 cal/g $^{\circ}$ C. You drop the metal into a 500 g calorimeter containing 75 g of water at 20 $^{\circ}$ C. The calorimeter is constructed of a material that has a specific heat of 0.10 cal/g $^{\circ}$ C. When equilibrium is reached, what will be the final temperature?

In Class Group Problem 15.13:

An 80 g piece of copper, initially at 295 $^{\circ}$ C, is dropped into 250 g of water contained in a 300 g aluminum calorimeter; the water and calorimeter are initially at 10 $^{\circ}$ C. What is the final temperature of the system? $c_{Cu} = 0.0920$ cal/g $^{\circ}$ C, $c_{Al} = 0.215$ cal/g $^{\circ}$ C

In Class Group Problem 15.14:

A 3.0 g lead bullet is traveling at a speed of 240 m/s when it embeds in a block of ice at 0 $^{\circ}$ C. If all the heat generated goes into melting the ice, how many kg of ice are melted? $c_{lead}$ = 0.0305 kcal/kg $^{\circ}$ C, $L_f = 3.34 \times 10^5$ J/kg

In Class Group Problem 15.15:

Iced tea is made by adding ice to 1.8 kg of hot tea, initially at 80 $^{\circ}$ C. How many kg of ice, initially at 0 $^{\circ}$ C, are required to bring the mixture to 10 $^{\circ}$ C? Assume water and tea have the same specific heat. $L_f = 3.34 \times 10^5$ J/kg

In Class Group Problem 15.16:

You add 0.200 kg of ice at -15 $^{\circ}$ C to 1.30 kg of water vapor at 120 $^{\circ}$ C.

$L_f = 3.34 \times 10^5$ J/kg, $L_v = 2.26 \times 10^{6}$ J/kg, $c_{ice} = 2093$ J/kg $^{\circ}$ C, $c_{water} = 4186$ J/kg $^{\circ}$ C, $c_{steam} = 1996$ J/kg $^{\circ}$ C

(a) How much energy is required to heat up the ice to 0 $^{\circ}$ C?

(b) How much energy is required to melt the ice?

(c) How much energy is required to heat the former ice, now water, to 100 $^{\circ}$ C?

(d) How much energy will you produce by cooling the water vapor to 100 $^{\circ}$ C?

(e) The energy lost by the steam is gained by the ice. How many kg of steam would have to turn into water through the latent heat of vaporization to finish the job of turning the former ice into water at 100 $^{\circ}$ C?

(f) The system has now reached equilibrium after the above steps. How much of the water is now in ice form? How much in water form? How much in vapor form?

In Class Group Problem 15.17:

You place a 500 g ice cube at 0 $^{\circ}$ C in a styrofoam box with wall thickness 1.0 cm and total surface area 600 cm $^2$ . Assume the ice cube originally takes up the entire volume of the box. If the air surrounding the box is at 20 $^{\circ}$ C and after 4 hours, the ice is completely melted, what is the conductivity of styrofoam?

In Class Group Problem 15.18:

You are helping a friend who is a veterinarian to do some minor surgery on a cow. She has asked you to sterilize a scalpel and a hemostat by boiling them for 30 minutes. You boil them as ordered and then quickly transfer the instruments to a well insulated tray containing 200 grams of sterilized water at room temperature(23 $^{\circ}$ C), which is just enough to cover the instruments. After a few minutes the instruments and water will come to the same temperature, but will they be safe to hand to your friend without being burned? You are both wearing surgical rubber gloves, but they are very thin. You know that both the 50 gram scalpel and the 70 gram hemostat are made from steel which has a specific heat of 450 J / (kg $^{\circ}$ C). They were boiled in 2.0 kg of water with a specific heat of 4200 J / (kg $^{\circ}$ C).

In Class Group Problem 15.19:

You have a summer job with a company that designs cookware. Your group is assigned the task of designing a better pasta pot. You are very excited by a new strong, light alloy the group has just produced, but will it make a good pasta pot? If it takes more than 10 minutes to boil water in a pasta pot, it probably won’t sell. So your boss asks you to calculate how long it would take water at room temperature (23 $^{\circ}$ C) to reach boiling temperature (100 $^{\circ}$ C) in a pot made of the new alloy. Your colleagues tell you that a typical pasta pot holds about 2 liters (2.0 kg) of water. They estimate that a pot made of the alloy would have a mass of 550 grams, and a specific heat capacity of 860 J / (kg $^{\circ}$ C). You look in your physics book and find that water has a specific heat capacity of 4200 J / (kg $^{\circ}$ C) and its heat of vaporization is 2.3 $\times 10^6$ J/kg. The owner’s manual states that the burners on your stove deliver 1000 Joules of heat per second. You estimate that only about 20% of this heat is radiated away.

In Class Group Problem 15.20:

This problem requires both mechanical energy and heat energy for a solution. In the class demonstration, a 2.0-gram lead bullet was shot into a 2.0-kg block of wood. The block of wood with the bullet stuck in it was hung from a string and rose to a height 0.50 cm above its initial position. From that information we calculated that the initial speed of the bullet was about 500 m/s (close to the speed of sound). If all the energy that didn’t go into lifting the block went into heating the bullet, what was the temperature change of the bullet? Assume that the bullet had a temperature of 50 $^{\circ}$ C when it left the gun. The melting temperature of lead is 330 $^{\circ}$ C. It has a specific heat capacity of 130 J/(kg $^{\circ}$ C) and a latent heat of fusion of 25 J/g. The specific heat capacity of wood is 1700 J/(kg $^{\circ}$ C).

Practice Exam Question 15.1: