6 Chapter 6: Frictional Forces
Textbook Chapter 6: Applications of Newton’s Laws
Section 6.1: Frictional Forces
Textbook Section 6.2: Friction
Friction is a force that opposes motion. Friction always acts in the direction opposite that of the motion. Kinetic friction occurs between two surfaces that are moving relative to each other, such as a box sliding down a ramp or a skier on a slope. Static friction occurs between surfaces that are not moving relative to each other, such as a person standing stationary on a ramp.
In general, the force of static friction (measured through the use of a unit less constant called the coefficient of static friction) will be greater than the force of kinetic friction (using the coefficient of kinetic friction). You might have already noticed this in everyday life — it’s harder to get a shopping cart moving once it’s stationary, but easy to keep it moving once it’s rolling. That’s the difference between static and kinetic friction.
Surfaces are rough up close, no matter how finely polished something is. These rough patches come into contact and force other rough patches to move over them in a non-uniform matter, causing friction. Static friction is greater than kinetic friction because surfaces in contact for even a short amount of time without moving tend to develop chemical bonds with the other surface, which must be broken in order to allow the surfaces to move relative to each other.
The force of static friction is calculated as following:
![]()
Why the less than or equal to sign? When ![]() , the object will just barely begin to move. This is the point where the normal force overcomes the static friction force. When the normal force is smaller, static friction will dominate.
, the object will just barely begin to move. This is the point where the normal force overcomes the static friction force. When the normal force is smaller, static friction will dominate.
The force of kinetic friction is calculated as:
![]()
Note that the coefficients of kinetic and static friction carry no units.
Section 6.2: Drag Forces
Textbook Section 6.4: Drag Force and Terminal Speed
Drag is an opposing frictional force due to an object moving through a fluid (air, water, gas cloud, liquid metal, etc). The drag force is calculated as:
![]()
where ![]() is our drag force opposing the direction of motion,
is our drag force opposing the direction of motion, ![]() is a drag coefficient (must be measured for every object),
is a drag coefficient (must be measured for every object), ![]() is the density of the fluid the object is moving through (where
is the density of the fluid the object is moving through (where ![]() = mass / volume),
= mass / volume), ![]() is the area of the object in contact with the fluid, and
is the area of the object in contact with the fluid, and ![]() is the velocity at which the object moves through the fluid.
is the velocity at which the object moves through the fluid.
When an object is falling through a fluid, it will eventually reach a \emph{terminal velocity} where the upwards drag force ![]() is equal to the downwards gravitational force
is equal to the downwards gravitational force ![]() . At this point, the object has a single velocity and does not accelerate any further. The terminal velocity is calculated as:
. At this point, the object has a single velocity and does not accelerate any further. The terminal velocity is calculated as:
![]()
In Class Group Problem 6.1:
A 23.5 kg box is placed on a ramp as shown below. The box is released from rest and reaches a velocity of 2.61 m/s by the time it reaches the bottom of the ramp. What is the coefficient of kinetic friction between the ramp and the box?
Don’t worry about static friction, assume the box starts moving immediately. The length of the box doesn’t matter; treat it like a point starting at the top of the ramp.
In Class Group Problem 6.2:
After moving out on your own, you buy a mattress but are too broke to pay for delivery. Instead, you put the mattress on the roof of your car to drive home at a relatively slow velocity of 15 m/s. You see a red traffic light coming up and hit the brakes. If the coefficient of static friction between the mattress and the car roof is 0.700, what is the minimum stopping distance you can use to keep the mattress from falling off your roof?
In Class Group Problem 6.3:
The Empire State Building is 1,454 ft tall.
If you dropped a penny off the observation deck, how fast would it be moving by the time it hit the pavement below? Ignore friction for this calculation.
A penny minted this year has a mass of 2.5 g, a diameter of 0.75 inches, and a thickness of 0.0598 inches. What is the cross-sectional area of a penny dropped face down? How about edge down?
Find the terminal velocity of the penny in each situation in part (b) if the drag coefficient is 0.5. The density of air is ![]() kg/m
kg/m![]() .
.
How long does it take the penny to reach the ground in each case?
Your edge-down penny hits the head of an unfortunate person walking down the sidewalk. The skin of the scalp is 8 mm thick, causing the penny to come to a stop. How much force is exerted on the person’s head? Is it enough to crack the skull (2,300 N or higher)?
In Class Group Problem 6.4:
On Star Trek: The Next Generation, a race called the Borg built cube-shaped space ships with an approximate volume of 28 km![]() . The density of the interstellar medium (space between stars) is about 20 hydrogen atoms per cubic centimeter (1 hydrogen atom has a mass of 1.66
. The density of the interstellar medium (space between stars) is about 20 hydrogen atoms per cubic centimeter (1 hydrogen atom has a mass of 1.66![]() kg). Calculate the drag force experienced by the Borg cube as it moved through space at 0.90
kg). Calculate the drag force experienced by the Borg cube as it moved through space at 0.90![]() (
(![]() m/s, the speed of light in a vacuum). Assume
m/s, the speed of light in a vacuum). Assume ![]() = 1.0 for a Borg cube.
= 1.0 for a Borg cube.
In Class Group Problem 6.5:
You are driving your car uphill along a straight road. Suddenly, you see a car run a red light and enter the intersection just ahead of you. You slam on your brakes and skid in a straight line to a stop, leaving skid marks 100 feet long. A policeman observes the whole incident and gives a ticket to the other car for running a red light. He also gives you a ticket for exceeding the speed limit of 30 mph. When you get home, you read your physics book and estimate that the coefficient of kinetic friction between your tires and the road was 0.60, and the coefficient of static friction was 0.80. You estimate that the hill made an angle of about 10![]() with the horizontal. You look in your owner’s manual and find that your car weighs 2,050 lbs. Will you fight the traffic ticket in court?
with the horizontal. You look in your owner’s manual and find that your car weighs 2,050 lbs. Will you fight the traffic ticket in court?
In Class Group Problem 6.6:
You are planning to build a log cabin in northern Vermont. You will pull the logs for the cabin up a long, smooth hill to the building site by means of a rope attached to a winch. You need to buy a rope for this purpose, so you need to know how strong the rope must be. Stronger ropes cost more. You know that the logs weight a maximum of 200 kg. You measure that the hill is at an angle of 30![]() with respect to the horizontal, and the coefficient of kinetic friction between a log and the hill is 0.90. When pulling the log up the hill, you will make sure that the rope stays parallel to the surface of the hill and the acceleration of the log is never more than 0.80 m/s
with respect to the horizontal, and the coefficient of kinetic friction between a log and the hill is 0.90. When pulling the log up the hill, you will make sure that the rope stays parallel to the surface of the hill and the acceleration of the log is never more than 0.80 m/s![]() . How strong of a rope should you buy?
. How strong of a rope should you buy?
In Class Group Problem 6.7:
Because of your physics background, you have been able to get a job with a company devising stunts for an upcoming adventure movie being shot in Rhode Island. In the script, the hero has been fighting the villain on the top of the locomotive of a train going down a straight horizontal track at 20 mph. He has just snuck on the train as it passed over a lake so he is wearing his rubber wet suit. During the fight, the hero slips and hangs by his fingers on the top edge of the front of the locomotive. The locomotive has a smooth steel front face sloped at 20![]() from the vertical so that the bottom of the front is more forward that the top. Now the villain stomps on the hero’s fingers so he will be forced to let go and slip down the front of the locomotive and be crushed under its wheels. Meanwhile, the hero’s partner is at the controls of the locomotive trying to stop the train. To add to the suspense, the brakes have been locked by the villain. It will take her 10 seconds to open the lock. To her horror, she sees the hero’s fingers give way before she can get the lock off. Since she is the brains of the outfit, she immediately opens the throttle causing the train to accelerate forward. This causes the hero to stay on the front face of the locomotive without slipping down giving her time to save the hero’s life. The movie company wants to know what minimum acceleration is necessary to perform this stunt. The hero weighs 180 lbs. in his wet suit. The locomotive weighs 100 tons. You look in a book giving the properties of materials and find that the coefficient of kinetic friction for rubber on steel is 0.50 and its coefficient of static friction is 0.60.
from the vertical so that the bottom of the front is more forward that the top. Now the villain stomps on the hero’s fingers so he will be forced to let go and slip down the front of the locomotive and be crushed under its wheels. Meanwhile, the hero’s partner is at the controls of the locomotive trying to stop the train. To add to the suspense, the brakes have been locked by the villain. It will take her 10 seconds to open the lock. To her horror, she sees the hero’s fingers give way before she can get the lock off. Since she is the brains of the outfit, she immediately opens the throttle causing the train to accelerate forward. This causes the hero to stay on the front face of the locomotive without slipping down giving her time to save the hero’s life. The movie company wants to know what minimum acceleration is necessary to perform this stunt. The hero weighs 180 lbs. in his wet suit. The locomotive weighs 100 tons. You look in a book giving the properties of materials and find that the coefficient of kinetic friction for rubber on steel is 0.50 and its coefficient of static friction is 0.60.
Practice Exam Question 6.1:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
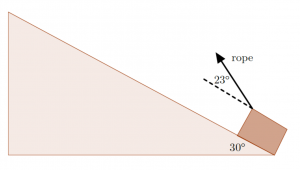
During a strong-man competition, Augustus pulls a 45 kg box up a 30![]() incline by a rope inclined at 23
incline by a rope inclined at 23![]() to the slope. He starts from rest and reaches the top of the 7.0 m high incline after 18 seconds.
to the slope. He starts from rest and reaches the top of the 7.0 m high incline after 18 seconds. ![]() = 0.270. Ignore static friction. What was the tension
= 0.270. Ignore static friction. What was the tension
in the rope?
Practice Exam Question 6.2:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
While visiting a friend in San Francisco you decide to drive around the
city. You turn a corner and are driving up a steep hill. Suddenly, a small boy runs out on the street chasing a ball. You slam on the brakes and skid to a stop leaving a 15 m long skid mark on the street. The boy calmly walks away but a policeman watching from the sidewalk walks over and gives you a ticket for speeding. You are still shaking from the experience when he points out that the speed limit on this street is 25 mph. After you recover your wits, you examine the situation more closely. You determine that the street makes an angle of 20![]() with the horizontal and that the coefficient of kinetic friction between your tires and the street is 0.60. Your car’s information book tells you that the mass of your car is 1570 kg. You weigh 85 kg. Will you fight the ticket in court?
with the horizontal and that the coefficient of kinetic friction between your tires and the street is 0.60. Your car’s information book tells you that the mass of your car is 1570 kg. You weigh 85 kg. Will you fight the ticket in court?
Practice Exam Question 6.3:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
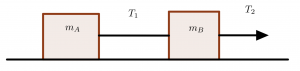
Two boxes, ![]() kg and
kg and ![]() kg, are attached by a string under tension
kg, are attached by a string under tension ![]() . The right-most box is being pulled horizontally across the floor by a different string under tension
. The right-most box is being pulled horizontally across the floor by a different string under tension ![]() . The coefficient of kinetic friction between the boxes and the floor is
. The coefficient of kinetic friction between the boxes and the floor is ![]() . If the boxes are accelerating at 3.5 m/s
. If the boxes are accelerating at 3.5 m/s![]() to the right, what is the tensions
to the right, what is the tensions ![]() and
and ![]() ?
?
Practice Exam Question 6.4:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
Practice Exam Question 6.5:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
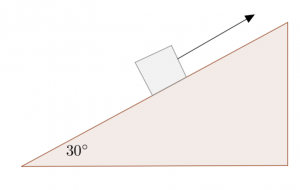
A mover has to move a heavy sofa of mass 62 kg to the second floor of the house. As he pulls on the rope tied to the sofa he makes sure that the rope is parallel to the surface of the ramp, which is at 30.0¡ to the horizontal. If the coefficient of kinetic friction between the sofa and the ramp is 0.300, and the sofa has an acceleration of 0.700 m/s![]() up the ramp, find the tension in the rope.
up the ramp, find the tension in the rope.
Practice Exam Question 6.6:
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
A person is pushing a heavy box down a ramp which is inclined to the horizontal at 13![]() . The box has a mass of 75 kg, and the person is pushing with a constant force of 65 N. If the box moves down the ramp at a constant velocity, what is the coefficient of kinetic friction between the box and the ramp?
. The box has a mass of 75 kg, and the person is pushing with a constant force of 65 N. If the box moves down the ramp at a constant velocity, what is the coefficient of kinetic friction between the box and the ramp?
A force that acts opposite the direction of motion. This is a contact force, and works parallel to the surfaces in contact.
The frictional force that occurs when one surface is moving relative to another.
Friction that occurs when two surfaces in contact are at rest relative to each other.