Chapter 7: Work and Energy

Adria Updike

7 Chapter 7: Work and Energy

Textbook Section 7.1: Introduction to Work and Energy

Section 7.1: Work and the Dot Product

Textbook Section 2.4: Products of Vectors

Work is defined as the change in kinetic energy (energy associated with motion) of an object. Work is calculated as the dot product (vector product) of two vectors we have already considered, force $\vec{F}$ and displacement $\vec{s}$ .

$W = \vec{F} \cdot \vec{s}$

Note that work $W$ is not a vector itself. The dot product of two vectors is a scalar quantity. Work can be positive or negative (work done on an object vs work done by an object has negative signs) but that is not considered a direction. Work has units of Joules (J) which are equivalent to Nm or kg m $^2$ /s $^2$ .

A dot product (also called a vector product) is equivalent to projecting one vector onto another vector and considering only the overlapping section. Thus,

$\vec{A} \cdot \vec{B} = A\, B \,cos\phi = \mid \vec{A} \mid \, \mid \vec{B} \mid \, cos\phi$

Therefore, the dot product between two vectors is the product of their magnitudes with the cosine of the angle between the vectors. In class, you will see how this can be expanded for vectors of the form $\vec{A} = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}$ . After the expansion, we find another way to write the dot product between vectors $\vec{A}$ and $\vec{B}$ ,

$\vec{A} \cdot \vec{B} = A_x B_x + A_y B_y + A_z B_z$

Note that when you add up these three terms (and you can, because none of them carry directional information due to the fact that $\hat{i} \times \hat{i}$ = 1) you are left with a single scalar number with no directional information past positive or negative (but it still has units!).

If you are working with magnitudes and displacements of vectors of force and displacement, use $W = F \,s \,cos \phi$ . If you are working with full vector forms of $\vec{F}$ and $\vec{s}$ , use $\vec{A} \cdot \vec{B} = A_x B_x + A_y B_y + A_z B_z$ instead.

If you do work (say, by pushing an object) in the direction of $\vec{s}$ (the direction in which it is traveling) then you are doing positive work on the object, and it will speed up as a result. If you give the object a push in the direction opposite its motion, it will instead slow down or turn around, and you have done negative work on the object. When the push is directed perpendicular to the direction of motion, it has no effect on the velocity (cos 90 = 0).

Section 7.2: Kinetic Energy

Textbook Section 7.2: Kinetic Energy

Textbook Section 7.3: The Work-Energy Theorem

Energy is defined as the ability to do work. Energy is not a tangible thing (you can’t have a bowl full of energy) but instead of property of an object due to its position relative to some other object or point in space. The closest thing we have to a packet of pure energy is a photon (light particle) which carries energy from one point to another (like the ultraviolet radiation from the Sun which is absorbed by your skin).

Energy is a conserved quantity — there is no net loss or gain of energy as far as the universe is concerned. There’s a certain amount of energy out there, and that’s all we’ve got to work with. However, energy can transform from one form to another, something we’ll see quite often in this class, without any net loss of total energy. Kinetic energy is turned into potential energy as you climb up a flight of stairs. Potential turns back into kinetic as you dive into a pool of water. Energy stored in your cells as food turns into heat when you exercise. And the Sun turns hydrogen into energy through the process of nuclear fusion according to Einstein’s famous equation $E = mc^2$ . All forms of energy (kinetic, spring potential, gravitational potential, and so on) are measured in units of Joules (J).

When we do work on a system, by giving it a push or changing its position, we are transferring energy into or out of that system. We will see in class that

$W = \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2$

or work is defined as the change in kinetic energy of a system (final minus initial) where

$KE = 1/2 \,m v^2$

is the kinetic energy (energy associated with motion). A perfectly still object with velocity equal to zero has no kinetic energy.

The Work-Energy Theorem relates work and kinetic energy by saying that $W = KE_f - KE_i = \Delta KE$ .

So far we have been considering cases of a constant force (due to gravity, or an engine). What about cases of a varying force? The spring force is a good example of a varying force. The further you extend a spring (pull the ends apart), the stronger you must pull in order to extend it any further. It turns out that if you graph the distance $\Delta x$ that you have extended or displaced an object vs the force $F$ you applied to cause that extension, the work you have done on the object is the area under the $F-s$ graph. For a constant force, the force does not change and the area under the graph is simply $F \,s$ . For a varying force, you must integrate to find the area under the curve.

$W = \int^{x_2}_{x_1} F \,x\, dx$

This is the official definition of work, but for cases in which we have a constant force (most cases) we only have to worry about the definitions given earlier (equations 2 and 3).

Kinetic energy is another scalar quantity, like work. You can simply add energies together without worrying about their directions (not a vector sum). However, unlike work and potential energy (coming up next) kinetic energy will always be a positive number. That’s because the mass $m$ is always positive, and squaring the initial and final velocities $v$ will always make them positive as well.

Section 7.3: Gravitational Potential Energy

Textbook Section 8.1: Potential Energy of a System

While kinetic energy KE is energy associated with an object because of its velocity, potential energy PE is energy associated with an object due to its position in space defined relative to an arbitrary zero point. This means that potential energy itself is a somewhat arbitrary definition, but typically we’re only dealing with the change in potential energy, and that remains constant no matter where you place your zero point. It all works out in the end.

The potential energy of an object due to its position with respect to gravity, called the gravitational potential energy $PE_g$ , is given as

$PE = mgh$

where $m$ is the mass of the object, $g$ = 9.81 m/s $^2$ on the surface of the Earth, and $h$ is the distance above or below some zero point (which can be positive or negative). $h$ is often substituted with $y$ . Potential energy is also related to work through the work-energy theorem (but with a negative sign), giving us the following useful equation called the conservation of mechanical energy equation:

$PE_{g,i} + KE_i = PE_{g,f} + KE_f$

or also stated as

$m g y_i + \frac{1}{2} m v_i^2 = m g y_f + \frac{1}{2} m v_f^2$

Note that when plugging $g$ into the potential energy equation, the negative sign on the $g$ has already been taken care of. $g$ is now a positive 9.81 m/s $^2$ . It always helps simplify your equations if you can take either $y_i$ or $y_f$ as equal to zero. As long as you keep the distance between them constant, it doesn’t matter what you call $y_i$ and $y_f$ .

In Class Group Problem 7.1:

A force $\vec{F}$ = (2.9 N) $\hat{i} - (5.2 N)\hat{j}$ is applied to an object with a displacement $\vec{r}$ = (-4.7 m) $\hat{i}$ + (1.2 m) $\hat{j} - (8.6$ m) $\hat{k}$ . What is the work done on the object?

In Class Group Problem 7.2:

You pick up a 13.5 kg box from the floor, lift it up to 1.2 m, carry it 25 m north, and set it down on a table 0.82 m off the ground. How much work did you do on the box?

In Class Group Problem 7.3:

The box in the image below is moving to the right at a constant velocity. A force is applied to the box in five different ways. Rank the boxes shown from the most positive work done to the most negative work done on the box as a result of the applied force.

In Class Group Problem 7.4:

A hockey puck with a mass of 170 g is moving across the frictionless ice at 5.0 m/s. A force is applied by a hockey stick opposite the direction of the puck’s motion, resulting in the puck moving at 2.5 m/s in the opposite direction.

What were the initial and final kinetic energies of the puck?

If the stick applied the force over a distance of 0.5 cm, what was the applied force?

In Class Group Problem 7.5:

You throw a 2 kg ball into the air at 12 m/s. Use conservation of mechanical energy to determine the maximum height above your hand the ball will reach.

In Class Group Problem 7.6:

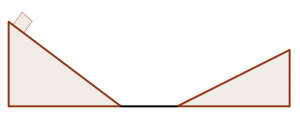
A block starts out at rest at the top of the left-hand ramp below, which has a height of 3.0 meters at an angle of 15 $^{\circ}$ with respect to the horizontal. The block and the ramp have a coefficient of kinetic friction of 0.150. The block slides down the left-hand ramp, across the frictionless floor to the frictionless right-hand ramp (at an angle of 12 $^{\circ}$ with the horizontal) and slides up the right-hand ramp. How far up the right-hand ramp will the block slide before coming to a halt and turning around?

In Class Group Problem 7.7:

You are driving your car uphill along a straight road. Suddenly, you see a car run a red light and enter the intersection just ahead of you. You slam on your brakes and skid in a straight line to a stop, leaving skid marks 100 feet long. A policeman observes the whole incident and gives a ticket to the other car for running the red light. He also gives you a ticket for exceeding the speed limit of 30 mph. When you get home, you read your physics book and estimate that the coefficient of kinetic friction was 0.80. You estimate that the hill made an angle of about 10 $^{\circ}$ with the horizontal. You look in your owners manual and find that your car weighs 2,050 lbs. Will you fight the traffic ticket in court?

In Class Group Problem 7.8:

You have landed a summer job with a company that has been given the contract to design the ski jump for the next Winter Olympics. The track is coated with snow and has an angle of 25 $^{\circ}$ from the horizontal. A skier zips down the ski jump ramp so that he leaves it at high speed. The winner is the person who jumps the farthest after leaving the end of the ramp. Your task is to determine the height of the starting gate above the end of the ramp which will determine the mechanical structure of the sky jump facility. You have been told that the typical ski-jumper pushes off from the starting gate at a speed of 2.0 m/s. For safety reasons, your design should be such that for a perfect run down the ramp, the skier’s speed before leaving the end of the ramp and sailing though the air should be no more than 80 km/hr. You run some experiments on various skis used by the jumpers and determine that the coefficient of static friction between the snow and the skis is 0.10 and its coefficient of kinetic friction is 0.02. Since the ski jumpers bend over and wear very aerodynamic suits, you decide to neglect the air resistance in your design.

Practice Exam Question 7.1:

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

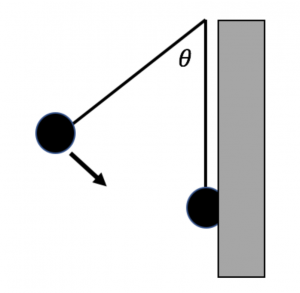
On an episode of Forensic Files, investigators want to know if the force a man suffered in a head-on collision was strong enough to break his glasses. They suspect he has faked his own death, as a pair of unbroken glasses was found near the scene. They know the person ran into the wall at 3.0 m/s. They put a similar pair of glasses on a 5.2 kg melon to simulate the person’s head, and attach the melon to a 3.4 m long rope hanging from the ceiling. They draw back the rope at an angle and let go. Ignore friction in this problem.

To which angle should they draw back the rope so that the melon runs into the wall at a velocity of 3.0 m/s? Solve this problem using conservation of energy.

The melon hits the wall and comes to a stop in a distance of 2.1 cm, during which the melon is crushed. If the melon and glasses suffer a force of greater than 320 N, the glasses will break. Determine the force the melon and glasses experience hitting the wall and coming to a stop. What force is exerted on the glasses? Will the glasses break?

License

Icon for the Creative Commons Attribution 4.0 International License