Chapter 5: Introduction to Forces

Adria Updike

5 Chapter 5: Introduction to Forces

Textbook Chapter 5: Newton’s Laws of Motion

Section 5.1: Newton’s First Law

Textbook Section 5.2: Newton’s First Law

A force is defined as a push or a pull on an object. This might be due to a direct interaction between two objects (contact force) or due to a long-range force such as gravity. The contact forces we will consider include the normal, friction, and tension forces.

We make a distinction between the mass and weight of an object. Mass is a measure of how much stuff is there; it is measured in kg (SI unit). Weight, on the other hand, is a force, not a measure of mass. Weight is calculated as mass times gravity ( $w = mg$ ). On Earth’s surface, with a constant gravitational force of 9.81 m/s $^2$ , we can convert back and forth between mass and weight. However, while your mass remains constant anywhere you go in the universe, your weight is constantly changing due to local gravitational forces.

Forces are vector quantities with both magnitude and direction. Forces are added as vectors.

Newton’s First Law: the law of inertia. An object in motion (has a constant or zero velocity) will remain in motion unless acted upon by an outside force.

Newton’s first law tells us that any change in velocity (magnitude, direction, or both) must be due to a force acting on the object. What forces might act on a book pushed across a table to bring it to a stop? These forces can include friction with both the table and the air (we will address frictional forces in Chapter 6). Our own experience tends to disagree with Newton’s first law because we are always in the presence of frictional forces on Earth. But if you threw a book into the emptiness of space, it would continue to move at the velocity you threw it until it ran into something. There’s nothing to slow it down.

Newton’s first law is only valid in inertial reference frames (where the object is not accelerating – moving at constant velocity or not moving at all). We will only consider these cases.

Section 5.2: Newton’s Second Law

Textbook Section 5.3: Newton’s Second Law

Newton’s Second Law: a net force on an object causes it to accelerate in the direction of the force ( $F = ma$ ).

Any change in the velocity (magnitude or direction or both) of an object is caused by a force, and the magnitude of that force is equal to the mass of the object times the acceleration of the object. Forces are measured in units of Newtons (N), which are equal to a kg m/s $^2$ .

Section 5.3: Newton’s Third Law

Textbook Section 5.5: Newton’s Third Law

Newton’s Third Law: if object A exerts a force on object B, object B exerts an equal and opposite force on object A.

This law refers to the interaction between two objects. If one person pushes something, the object pushes back. You feel this every time you interact with something — heavy objects put up a lot of resistance to motion, and lighter objects put up less resistance to motion, but everything pushes back at least a little bit.

These equal and opposite forces are called third-law pairs, or sometimes action-reaction pairs. Note these are always the same kind of force, and the pairs always invothird-law pairslve only the two objects at hand. $\vec{F}_{A \,on\,B} = \vec{F}_{B\,on\,A}$ . For example, the Earth is pulling down on you. This is a gravitational force due to the interaction of two objects with mass (you and the Earth). The third law pair to this is the pull of you up on the Earth. Yes, you do pull the Earth up towards you as the Earth pulls you down. Why don’t you see the Earth coming up to meet you, and instead interpret it as you falling to the Earth? It’s a difference in mass. Remember that $F = ma$ . Both of these forces are equal, but pointing in opposite directions. The Earth pulls you down, you pull the Earth up. Because the Earth is so much more massive than you ( $m_{Earth} >> m_{you}$ ), your acceleration must be much larger than the acceleration of the Earth ( $a_{you} >> a_{Earth}$ ) in order for $m_{Earth} a_{Earth} = m_{you} a_{you}$ .

A common mistake people make when interpreting the third law is to think that since the forces are equal and in opposite directions, the reactions of the two objects will be equal. This isn’t the case! If their masses are different, the objects will both have different accelerations. The more massive object has a small acceleration, and the less massive object has a much larger acceleration.

Another common mistake is to think that because two forces are of equal value and in opposite directions, they must be third-law pairs. This isn’t necessarily the case. Third law pairs are between two objects only. If there are more than two objects between these forces, it’s not a third law pair.

Section 5.4: Free Body Diagrams (FBDs)

Textbook Section 5.7: Drawing Free Body Diagrams

For any object, you can draw a free body diagram (FBD). The free body diagram represents the object as a point, and you include all the individual forces acting on the object. You do NOT include the total force acting on the object (which is instead the vector sum of all individual forces) and you do not include forces the object is asserting on other objects. Only forces directly acting on the object at hand are included.

Consider a can of soda resting on your desk. What forces are present? Gravity is pulling down on the soda can, and the desk is pushing up on the soda can. The sum of these two forces must be equal to zero if the soda can is not accelerating (and it’s not, it’s sitting still). Thus, these forces are of equal and opposite magnitudes. Are they third law pairs? No! One force is between the soda can and the Earth, and the other force is between the soda can and the desk. So where are our third-law pairs? You will never have a third law pair on a FBD. Since the FBD only includes forces acting on the object, it will not include any forces of the object acting on something else (which must be the case for the third law pairs). The third law pairs to the forces above would be the soda can pulling up on the Earth and the soda can pushing down on the desk. Your resulting FBD for the soda can is given below.

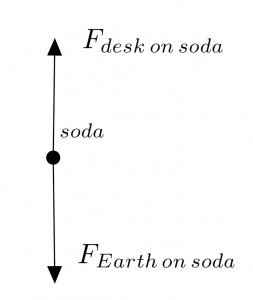
Because the upwards force of the desk on the soda is equal to the downwards force of the Earth on the soda, these two vectors should be given the same magnitude (length) in your drawing. If one force is bigger than another, make sure to indicate that in your FBD by the length of the vectors. Always label your vectors according to which force is acting on the object.

Section 5.5: Normal Forces

Textbook Section 5.6: Common Forces

What do we mean by a normal force? In this case, normal means perpendicular. Whenever you come into contact with an object (pushing on a door to open it, standing on a table or the ground, hitting a baseball with a baseball bat) you exert a normal force on that object (a force perpendicular to the surface of the object).

Think of the surface of any object (door, Earth, table, ball, etc.) like the rubber sheet of a trampoline. When you put an object on a trampoline, the surface deforms. But the trampoline has a restoring force associated with it, which acts like a spring when compressed. When you remove the object from the trampoline surface, the surface goes back to it’s normal state, a flat sheet. A heavier object deforms the surface further, while a light object only deforms the surface a little bit.

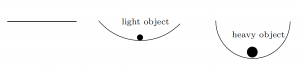
This restoring force is our normal force. Any force applied to an object, no matter how hard the surface of the object appears, deforms the surface in some way. This deformation leads to a restoring force that attempts to bring the surface back to where it was. When you push down on the ground, a restoring force called the normal force pushes back up.

There are limits to the normal force. You can only push down so far on some things before the normal force can no longer counter the applied force, and this is when objects break (like a table with an elephant on top).

Note that the normal force is special — it is however strong it needs to be to counter the applied force. Look at the objects on your desk — maybe you have a book, a computer, a pencil. The pencil has a smaller mass than the computer, so it applies a smaller force (the weight force, $F_{pencil}=m_{pencil}\,a_{gravity}$ ). The normal force of the table on the pencil only needs to counter the light weight of the pencil. But the normal force of the table on the computer has to counter the larger weight of the computer. The normal force for one object (the table) is not constant for all the objects acting on it (computer, book, pencil, etc.). The normal force is however large it needs to be in order to balance the opposing applied force.

A normal force always acts perpendicular to the surface which supplies the normal force. This does not mean the normal force is always perpendicular to the applied force. Consider a box sitting on a ramp. The force of gravity applies straight down, but the normal force from the ramp applies perpendicular to the ramp, not opposite the force of gravity. As a result, the gravitational and normal forces do not cancel out in this example. There is a net force in the direction down the ramp, and the box will experience an acceleration in that direction, which is why it will slide down the ramp.

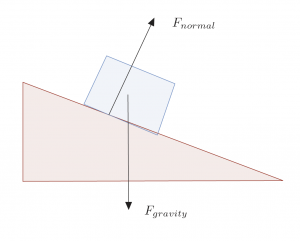
Section 5.6: Tension Forces

Textbook Section 5.6: Common Forces

Tension forces refer to forces applied to or by a string, chain, wire, etc. If you are hanging from a rope ladder above the ground, there is a tension force in the rope ladder equal to the force of gravity (assuming you haven’t fallen yet). But put too much force on the ladder (keep adding more weight) and it will eventually break. Everything that can give a tension force has a limit to how much it can take. That’s where the expression “you’re only as strong as your weakest link” comes from — the tension a chain of links can take is limited to the tension that can be applied to the weakest link of the chain. If one breaks, the tension is gone. In all of the problems we do, assume that the tension is equal along the entire rope/chain/etc.

Section 5.7: Solving Force Problems

Draw a picture.

Draw and label all forces acting on the object.

Pick a coordinate system. If there is a ramp involved, rotating your coordinate system to point up and down the ramp in the $x$ direction is a good idea. The problem will still work out the same way if you don’t do this and use the normal $x-y$ coordinate system, but doing the problem properly requires much more work if you don’t rotate your coordinate system (accelerations in both $x$ and $y$ directions). Pay attention to which forces are positive and which are negative in your coordinate system!

Draw a FBD for your object.

If you have any forces not lying directly along the $x$ or $y$ axes of your new coordinate system, you must break these forces into components in the $x$ and $y$ directions. Write the sum of the forces in each direction ( $F_{net,\,x}=, F_{net,\,y}=$ ). These sums are either equal to zero (all the forces balance out, no acceleration in this direction) or $ma$ (acceleration in that direction, unequal sum of forces).

Solve for whatever variable you are looking for using the equations you wrote in the previous step. Keep in mind you might need to use the kinematics equations as well.

In Class Group Problem 5.1:

A person pushes a box across a frictionless surface with a force of 12 N. If the box starts from rest and has reached a velocity of 3.5 m/s after 6.0 s, what is the mass of the box?

Draw a free body diagram (FBD) for the box and label all the forces acting on the box. Is the net force on the box equal to zero? In which direction does the net force point?

In Class Group Problem 5.2:

Bill weighs 220 lbs on the surface of the Earth. The Earth has a mass of 5.97 $\times 10^{24}$ kg.

What is Bill’s mass in kg?

Bill jumps off the roof of his car and suffers an acceleration of -9.8 m/s $^2$ towards the surface of the Earth. According to Newton’s third law, the Earth accelerates towards Bill such that the force of the Earth on Bill equals the force of Bill on the Earth. What acceleration does the Earth go through?

Why don’t we see the Earth moving up to meet us halfway as we fall towards it?

In Class Group Problem 5.3:

A car (3,200 lbs) driving at 45 m/s hits a mosquito (2.5 $\times 10^{-6}$ kg) moving in the opposite direction at 0.20 m/s. The mosquito is squished against the windshield in 0.10 s.

How does the force exerted by the mosquito on the car compare to the force exerted by the car on the mosquito?

Consider your answer to the previous question. Think about what happens to the mosquito. Explain why your answer makes sense in terms of Newton’s second law.

What is the change in acceleration of the car as a result?

In Class Group Problem 5.4:

A box is sitting at rest on a frictionless incline as shown below. A rope attached to the box (arrow) keeps it stationary. If the box has a mass of 35 kg, what is the tension in the rope (in other words, what force is it exerting to keep the box from moving)?

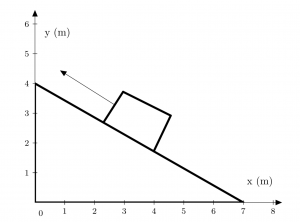
In Class Group Problem 5.5:

A 42 kg gymnast is dangling on a massless rope. Draw a FBD for the person and find the tension in the rope.

In Class Group Problem 5.6:

A 3.8 kg birdhouse is suspended from the roof by two massless ropes, $A$ and $B$ . A wind blowing to the left applies a constant force of 12 N. Draw a FBD for the birdhouse and find the tension in each rope if rope $A$ is 1.3 m long and rope $B$ is 2.7 m long. Assume the birdhouse is stationary.

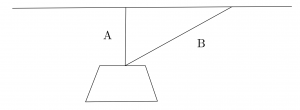
In Class Group Problem 5.7:

For the Atwood Machine shown below, $m_1$ has a mass of 2.00 kg and $m_2$ has a mass of 2.50 kg. Solve for the magnitude of the accelerations of $m_1$ , $m_2$ , and the tension in the cord connecting them over the pulley.

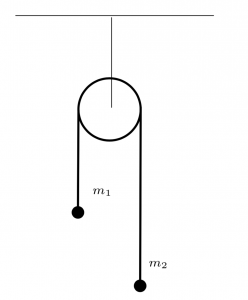
In Class Group Problem 5.8:

A box is sitting at rest at the top of a ramp 3.00 m long at an angle to the horizontal of 12 $^{\circ}$ . When the box reaches the bottom of the frictionless ramp, it falls an additional 2.00 m vertically before hitting the floor. How far from the right end of the ramp does the box fall (horizontal component)?

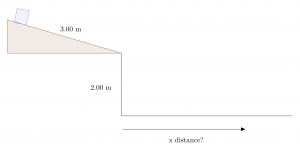
In Class Group Problem 5.9:

You are part of a design team for a new campus building. The project manager wants to suspend a 20-lb sculpture high over the room by hanging it from the ceiling using thin, clear fishing line (string) so that it will be difficult to see how the sculpture is held up. The only place to fasten the fishing line is to a wooden beam which runs around the edge of the room at the ceiling. The fishing line that she wants to use will hold 20 lbs so she suggests attaching two lines to the sculpture to be safe. Each line would come from the opposite side of the ceiling to attach to the hanging sculpture. Her initial design has one line making an angle of 20 $^{\circ}$ with the ceiling and the other making an angle of 40 $^{\circ}$ with the ceiling. She knows you took physics, and asks you if her design will work.

In Class Group Problem 5.10:

While driving in the mountains, you notice that when the freeway goes steeply downhill, there are emergency exits every few miles. These emergency exits are straight dirt ramps which leave the freeway and are sloped uphill. They are designed to stop trucks and cars that lose their breaks on the downhill stretches of the freeway even if the road is covered in ice. You are curious, so you stop at the next emergency road. You estimate that the road rises at an angle of 10 $^{\circ}$ from the horizontal and is about 300 ft long. What is the maximum speed of a truck that you are sure will be stopped by this road, even if the frictional force of the road surface is negligible?

In Class Group Problem 5.11:

While driving in the mountains, you notice that when the freeway goes steeply downhill, there are emergency exits every few miles. These emergency exits are straight dirt ramps which leave the freeway and are sloped uphill. They are designed to stop trucks and cars that lose their breaks on the down hill stretches of the freeway even if the road is covered in ice. You wonder at what angle from the horizontal an emergency exit should rise to stop a 50 ton truck going 70 mph up a ramp 300 ft long, even if the frictional force of the road surface is negligible.

License

Icon for the Creative Commons Attribution 4.0 International License