3 Chapter 3: One Dimensional Motion

Link to Chapter 3 of the textbook

Section 3.1: Kinematics

Textbook section 3.1

Khan Academy: Displacement, Velocity, and Time Videos

Kinematics is the study of how things move. Distance is how far you have moved along the path you took, and is often given the symbol d. Displacement is how far you moved from your initial position regardless of path (final minus initial position) and is calculated as:

    \[\Delta x = x_f - x_i\]

where \Delta x means the change in the x-position, x_f is the final position, and x_i is the initial position. Both distance and displacement are measured in meters (m) when doing most calculations in physics (but always check for the units the question is expecting if it gives them!).

Recall that a scalar quantity is something that has magnitude only (how much you have) and is always a positive number (a negative indicates direction). A vector quantity has both magnitude and direction (how much and where it’s going) and can be positive or negative. Distance is a scalar, and displacement is a vector.

 

Section 3.2: Speed and Velocity

Textbook section 3.2

Khan Academy: Displacement, Velocity, and Time Videos

Speed is a scalar quantity indicating how fast something is moving, but does not include information on the direction (always positive). Speed is calculated as distance over time (how far you went divided by how long it took). Velocity is a vector including directional information, and is calculated as the displacement over time (the total distance you moved from your initial position divided by how long it took to arrive at the final position).

Average velocity is calculated as the displacement over a given time period in units of m/s.

    \[v_{av} = \frac{x_f - x_i}{t_f - t_i} = \frac{\Delta x}{\Delta t}\]

 

Instantaneous velocity is the velocity at some particular instant in time. This is found by taking the limit of the average velocity as the time period goes to zero, which is the derivative of the expression for the position x as a function of the time t.

    \[v_x = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt}\]

 

Section 3.3: Position vs. Time Graphs

Position vs. time, also called x-t graphs, chart the position of an object on the vertical axis as a function of time on the horizontal axis. Caution: these are not maps of motion! Moving in the horizontal direction across the graphs is increasing in time, not position.

At every point on an x-t graph, a line can be drawn tangent to the point (a straight line that just touches but does not intersect the curve at that point). The slope of this tangent line is equal to the velocity. Why is this? Consider taking the slope of this line by picking two random points on the line with coordinates (x_1, y_1) and (x_2, y_2). Slope is calculated as rise (change in vertical position) over run (change in horizontal position), also written as (y_2 - y_1)/(x_2 - x_1), or \Delta x/\Delta t (because our vertical axis is x position and our horizontal axis is y position), which we have defined as our average velocity.

 

What happens as we choose these points closer and closer together? The value of (x_2 - x_1) will approach zero, effectively taking the limit as we go to zero. Assuming the two points are right on top of each other (x_2 - x_1 = 0) we find the instantaneous velocity, dx/dt.

The slopes of these tangent lines can be positive or negative. Moving from left to right, a positive slope gets steeper (like climbing up a mountain) and a negative slope goes down (sliding down a hill). The larger the value of the slope, the steeper the mountain gets. A large positive slope means the function is rapidly increasing, and a large negative slope means the function is rapidly decreasing. Note that this does not depend on whether the current value of the function is above or below the horizontal axis.

So what does the horizontal axis mean? When the curve is above the axis, the x value of the position of the object at that time is positive. When the curve is below the axis, the x value is negative.

Velocity was the rate of change of the position with respect to time, and acceleration is the rate of change of velocity with respect to time. The average acceleration over some non-zero time period t_2 - t_1 can be calculated as

    \[a_{av} = \frac{v_{xf} - v_{xi}}{t_f - t_i}\]

in units of m/s/s, also called m/s2. Note the subscripts on the velocities in the previous equation; we’re only working in one dimension for now, but we’ll move into multiple dimensions in the next chapter so let’s keep our x‘s and y‘s straight.

Section 3.4: Acceleration and the Kinematics Equations

Textbook section 3.3

Textbook section 3.4

Khan Academy: Acceleration Videos

Khan Academy: Kinematics Equations Videos

The instantaneous acceleration (acceleration at some particular instant in time, not over a range of times) is calculated as the limit of the change in velocity as the time interval approaches zero, or the derivative of the velocity with respect to time.

    \[a_x = \lim_{\Delta t \to 0} \frac{\Delta v_x}{\Delta t} = \frac{dv_x}{dt}\]

The velocity was equal to the slope of the x-t graph, and the acceleration is equal to the slope of the v_x-t graph.

We will only be dealing with cases of constant acceleration in this chapter. That means the acceleration is either positive, negative, or zero, but the a-t graph will always have a slope of zero (horizontal lines). Transitions from one value of the acceleration to another are said to happen instantaneously (although we know this is not the case physically, it certainly simples the problem, and is a very good approximation for something falling in a gravitational field).

There are three kinematics equations relate position, velocity, and acceleration with time. These three equations are derived from each other; any two will give the same result as the third, so your answers should always agree no matter which equation(s) you choose to use.

    \[v_x = v_{0x} + a_x t\]

    \[v_x^2 = v_{0x}^2 + 2 a_x \Delta x\]

    \[\Delta x = v_{0x} + \frac{1}{2} a_x t^2\]

Recall that \Delta x = x_f - x_i.

Section 3.5: Tips for Solving Kinematics Equations

Think about the question. What are you being asked to find? How can you go about this?

Draw a picture.

Pick a zero point and positive x direction.

Write down what you know and what you’re looking for.

Write down the three kinematics equations.

Pick an equation that has what you have and what you’re looking for, but no terms you don’t have or need.

Solve for the answer.

Check to see if your answer makes sense.

 

You can always avoid the quadratic equation by using the other two equations instead of the one that leads to a quadratic.

In Class Group Work Problem 3.1

You walk in a straight line 300 m north, and the turn around and walk 470 m south. Draw a picture and label the north direction as positive.

What was the total distance you walked?

What was your total displacement?

What is the magnitude of your displacement?

In Class Group Work Problem 3.2

Kevin walks 3.4 km east, 6.1 km north, and 1.2 km west.

What distance did he walk?

What was his displacement?

 

In Class Group Work Problem 3.3

Janet runs around a circular track with a diameter of 0.50 km. If she does a total of four laps around the track in 1.5 hours,

what was her average speed in m/s?

What was her average velocity in m/s?

In Class Group Work Problem 3.4

Bill starts at x = 1 m. He walks south for two seconds and ends up at x = -2 m. Then he walks north at 1 m/s for three seconds, stands still for a second, and walks to x = 0, arriving 2 seconds later. Draw his motion on the x-t graph below.

In Class Group Work Problem 3.5

Label each line segment with a short description of Emily’s motion at that time.

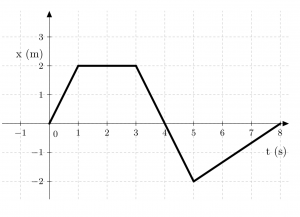
What was Emily’s average velocity between t = 0 and t = 3 s?

What was Emily’s instantaneous velocity at t = 4.5 s, 2 s, and 6 s?

Draw the v-t graph for Emily’s instantaneous velocity as a function of time on the graph below.

In Class Group Work Problem 3.6

Herbert’s motion as a function of time can be described by the function x(t) = (3.2 {\rm \, m}) + (0.75 \,t ) {\rm \, m/s} - (0.033\, t^2) {\rm \, m/s}^2.

Where (in x) would you find Herbert at t = 3.7 s?

Derive an equation for Herbert’s instantaneous velocity as a function of time, v_x(t).

How fast is Herbert moving after 11 s?

What is Herbert’s acceleration as a function of time, a_x(t)?

What is Herbert’s instantaneous acceleration at t = 0.80 s?

In Class Group Work Problem 3.7

A plane starts from rest and has reached a velocity of 85 m/s after 19 seconds. What was its acceleration?

In Class Group Work Problem 3.8

A rock falls off a cliff 85.0 m above the ground. Assume the acceleration due to gravity is -9.8 m/s^2.

How fast is the rock moving three seconds later?

How fast is the rock moving just before it hits the ground?

How long does it take the rock to hit the ground?

Practice Exam Question 3.1

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

Beth is playing with her remote controlled car. At time t = 0 s, she starts the car at x = 3 m, leaves it there for two seconds, drives it in the negative direction at -2 m/s until it reaches x = -1 m, then drives it at 1 m/s for three seconds, then drives until it reaches x = 0 m at t = 10 seconds.

Draw the motion of the car on the axes below.

What was the average velocity of the car between t = 0 s and t = 10 s?

What was the average velocity of the car between t = 1 s and t = 5 s?

What was the instantaneous velocity of the car at t = 6 s?

What was the instantaneous velocity of the car at t = 1 s?

Practice Exam Question 3.2

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

The position of an object is given by the equation x(t) = (-3 m/s^2) t^2 +(8 m/s^3) t^3 + 2 m.

Where is this object located at t = 5 seconds?

Derive the equation for the velocity of the object as a function of time.

What is the velocity of the object at t = 3 s?

Derive an equation for the acceleration of the object as a function of time.

What is the acceleration of the object at t = 4 s?

Practice Exam Question 3.3

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

A concussion is a traumatic brain injury caused by a rapid acceleration of the skull, causing the brain to hit the inside of the skull and damage the soft tissue of the brain. Concussions are thought to become severe around 90 g‘s of acceleration (where 1 g = 9.81 m/s^2).

Infants are especially prone to concussions. Suppose a young child is left momentarily unattended on a bed. The child may roll off the bed and fall onto the floor. Two common types of floor coverings are carpet and hardwood. A typical carpet can be compressed by 2.5 cm. Hardwood floor, on the other hand, can only be compressed around 1.5 mm. Let’s say a child falls off the edge of a bed, 3 feet above the floor. Assume the initial velocity of the child is 0 m/s. Will the child suffer a concussion on a carpeted floor? What about a hardwood floor?

Practice Exam Question 3.4

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

For a class project, your roommate builds a small rocket and launches it from the soccer field. The rocket has an initial velocity of zero, and begins to head straight upwards when its boosters fire. The boosters give the rocket an upwards acceleration of 6 m/s^2 for the first 5 seconds, then cut out. How high does the rocket go, and how long does it take it to hit the ground after it launches?

Practice Exam Question 3.5

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

In your new job, you are the technical advisor for the writers of a gangster movie about Bonnie and Clyde. In one scene Bonnie and Clyde try to flee from one state to another. (If they got across the state line, they could evade capture, at least for a while until they became Federal fugitives.) In the script, Bonnie is driving down the highway at 108 km/hour, and passes a concealed police car that is 1 kilometer from the state line. The instant Bonnie and Clyde pass the patrol car, the cop pulls onto the highway and accelerates at a constant rate of 2 m/s^2. The writers want to know if they make it across the state line before the pursuing cop catches up with them.

Practice Exam Question 3.6

These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.

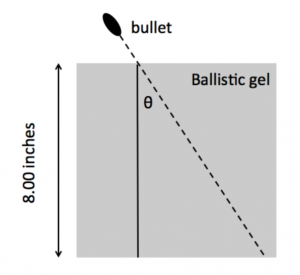
A bullet is fired through a piece of ballistic gel 8.00 inches long so that the bullet passes through the gel in a straight line along the dotted path below. The dotted path is at an angle of 41^{\circ} to the solid horizontal line. If the bullet had an initial speed of 5.00 \times 10^2 m/s and leaves the cardboard with a velocity of 4.00 \times 10^2 m/s,

find the acceleration of the bullet as it passes through the gel (assume the acceleration is constant and ignore gravity).

Find the total time the bullet is in contact with the gel.

definition

License

Icon for the Creative Commons Attribution 4.0 International License

Introductory Physics Resources Copyright © by Adria C Updike is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book