4 Chapter 4: Two Dimensional Motion
Section 4.1: Motion in Two and Three Dimensions
We began in the last chapter with the most simple kind of motion – motion in a straight line. Now we’re going to generalize this motion from a single dimension (up/down, left/right, or forward/back) to combinations of all of these dimensions. We’ll use the same three kinematics equations to describe this motion, but now instead of restricting ourselves to one direction at a time, we’ll use a combination of straight-line motion in two or three dimensions at once.
The important thing to realize here is that it’s the same motion we saw in the last chapter – we’re still moving at a constant acceleration, but now we might have different motion in the ![]() direction than we did in the
direction than we did in the ![]() direction. It’s vital to remember that changing your
direction. It’s vital to remember that changing your ![]() velocity, position, or acceleration does not change anything about your position, velocity, or acceleration in the
velocity, position, or acceleration does not change anything about your position, velocity, or acceleration in the ![]() and
and ![]() directions. The three directions are orthogonal to each other – changing one does not change the others.
directions. The three directions are orthogonal to each other – changing one does not change the others.
Because we will now be talking about motion in the ![]() ,
, ![]() , and sometimes
, and sometimes ![]() direction, we’re going to introduce a new way of writing position that doesn’t limit us to constantly referring to the
direction, we’re going to introduce a new way of writing position that doesn’t limit us to constantly referring to the ![]() direction. The new position vector
direction. The new position vector ![]() is written as:
is written as:
![]()
![]()
![]()
The three equations above are all equivalent ways of writing the position vector ![]() .
.
As a result, the displacement vector, the straight-line displacement between any two locations in three dimensions, is given by:
![]()
![]()
Now that we have a position vector, we can re-define our velocity vector ![]() in terms of the position vector.
in terms of the position vector.
![]()
![]()
![]()
The three equations above are equivalent statements of the velocity vector. Finally, we can do the same with the acceleration vector ![]() .
.
![]()
![]()
![]()
![]()
Textbook 4.1: Displacement and Velocity Vectors
Textbook 4.2: Acceleration Vector
Section 4.2: Projectile Motion
An object subject to a constant acceleration at an angle relative to its motion will move in a two-dimensional path known as its trajectory. Most of the objects we encounter will be subject to the constant acceleration due to the gravitational force. Any object subject to gravity is known as a projectile.
Two-dimensional kinematics works the same way as one-dimensional kinematics, but now acting in two orthogonal (perpendicular) directions. The important points to remember here are (1) that the ![]() and
and ![]() directions are orthogonal, which means they are perpendicular and that one does not rely on the other (a change in
directions are orthogonal, which means they are perpendicular and that one does not rely on the other (a change in ![]() does not mean you have aprojectile change in
does not mean you have aprojectile change in ![]() , and (2) that we will have a constant acceleration acting on our object, in either the
, and (2) that we will have a constant acceleration acting on our object, in either the ![]() direction, the
direction, the ![]() direction, or in some combination of the
direction, or in some combination of the ![]() and
and ![]() directions. Our derivation of the kinematics equations depended on a constant, non-changing acceleration.
directions. Our derivation of the kinematics equations depended on a constant, non-changing acceleration.
We again use the one-dimensional kinematics equations, but now we have one set in the ![]() direction and one set in the
direction and one set in the ![]() direction. The only variable they have in common is the time
direction. The only variable they have in common is the time ![]() measured in seconds.
measured in seconds.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Section 4.3: Kinematics Problem-Solving
We’ll start out using a set of steps to solve a kinematics problem. Often the hardest part in solving these problems is simply getting started, so use these steps as a road map.
Start by reading the problem.
Then, draw a picture. This doesn’t have to be super-accurate, but it should include everything involved in the problem. You might want to include labels for things and arrows indicating where things are going. Include the path you think objects will take.
Pick a coordinate system. Right now, a normal ![]() –
–![]() coordinate system is a good place to start. It doesn’t matter where you put the origin (
coordinate system is a good place to start. It doesn’t matter where you put the origin (![]() = 0,
= 0, ![]() = 0), you’ll get the same answer no matter where you put it, but some choices can make the problem a bit easier to solve, as you’ll discover. Draw the coordinate system on your picture.
= 0), you’ll get the same answer no matter where you put it, but some choices can make the problem a bit easier to solve, as you’ll discover. Draw the coordinate system on your picture.
Label things you know that appear in your equations – positions, velocities, accelerations. Write down what you know, and then, nearby, what you’re looking for.
Write down the kinematics equations.
Figure out how to get what you want out of what you have, now that you’ve got it all written out in front of you.
Let’s take a look at an example in one dimension.
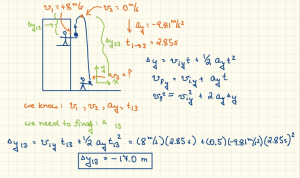
Suppose you’re standing in the window of your dorm room, and a friend is standing outside on the ground. You toss a ball straight up in the air at 8 m/s. 2.85 seconds later, your friend on the ground catches the ball. How far below you is your friend?
Start with a picture.
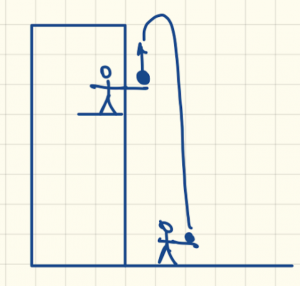
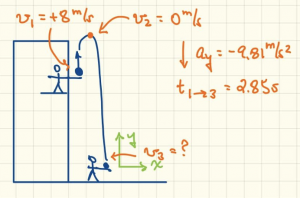
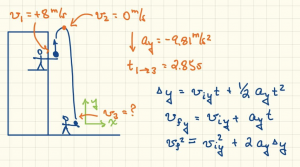
We will often deal with problems where we need to consider multiple time frames. If we see that ahead of time by drawing a picture and labeling it appropriately, it can make the problem easier to solve.
Here, we want to know the distance from me to my friend. That’s the same thing as the displacement of the ball from the beginning to end of it’s path. Alternatively, you could also solve this problem by determining how far up the ball goes until it reaches it’s apex, then subtract that from the distance it falls from there.
Either way you decide to solve this problem, you need to keep track of which position, velocity, and time you’re talking about. The kinematics equations apply to any one part of the problem, or the entire problem as a whole, but you need to make sure you’re not, say, trying to find the distance from ![]() (from your hand to the apex) by using the time between the apex and your friend’s hand (
(from your hand to the apex) by using the time between the apex and your friend’s hand (![]() . That’s not going to work out correctly! Whichever way you choose to solve this problem, make sure the positions and velocities and accelerations and times all correspond to the same interval!
. That’s not going to work out correctly! Whichever way you choose to solve this problem, make sure the positions and velocities and accelerations and times all correspond to the same interval!

In Class Group Problem 4.1
You kick a soccer ball. Its resulting trajectory is shown below. The ball moved from left to right. Three specific positions the ball passed through are labeled ![]() ,
, ![]() , and
, and ![]() .
. ![]() is the position of the ball as it leaves the ground, and
is the position of the ball as it leaves the ground, and ![]() is the position of the ball just before it hits the ground.
is the position of the ball just before it hits the ground.
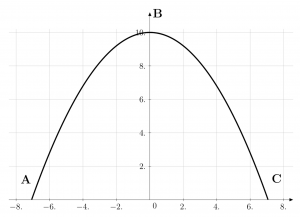
At which labeled position(s) has the ball reached its apex?
Draw the range of the maximum value of ![]() on the graph.
on the graph.
Draw the range of the maximum value of ![]() on the graph.
on the graph.
Where does the ball have the largest velocity? Why?
Where does the ball have the smallest velocity? Why?
Where does the ball feel the largest acceleration? Why?
The time it takes the ball to go from position ![]() to position
to position ![]() is
is ![]() . How long does it take the ball to go from position
. How long does it take the ball to go from position ![]() to position
to position ![]() ? How do you know?
? How do you know?
Under which circumstances would your answer to the previous question be incorrect?
In Class Group Work Problem 4.2
In Class Group Problem 4.3
A soccer player kicks the ball with an initial velocity of 17 m/s in the horizontal direction and 13 m/s in the vertical direction.
How fast is the ball moving when it hits the ground? Assume it hits the ground at the same level at which it left the ground. Note: the answer is not zero! ![]() is always the velocity just before you hit the ground.
is always the velocity just before you hit the ground.
How long was the ball in the air?
How high did the ball get above the ground?
How far did the ball travel in the ![]() direction?
direction?
Why can’t you assume that ![]() is equal to zero?
is equal to zero?
In Class Group Problem 4.4
A golf ball is hit at an angle of 25![]() and an initial velocity of 45 m/s. 2.5 seconds later, the ball hits the side of a building.
and an initial velocity of 45 m/s. 2.5 seconds later, the ball hits the side of a building.
What were the initial velocities of the ball in the ![]() and
and ![]() directions,
directions, ![]() and
and ![]() ?
?
Did the ball hit the building before or after it reached its peak in the ![]() direction? Show your work when answering this question.
direction? Show your work when answering this question.
How far had the ball traveled in the ![]() and
and ![]() directions when it hit the building?
directions when it hit the building?
In Class Group Problem 4.5
Arya is trying to jump her horse over a canyon. If the horse is running at 11 m/s and runs off the cliff horizontally, as least how far down does the next cliff 6.5 m away need to be in order for her to safely make the jump?
Draw a picture of this situation and label everything you know. Check your picture with others at your table before moving on to make sure you all agree.
How far down does the other side of the cliff need to be for her to just barely make the jump?
In Class Group Problem 4.6
At the Bristol 4th of July carnival, you can win a stuffed panda bear if you manage to toss a quarter into a cup on a shelf. The shelf is 2.5 m away from you. If you toss the quarter with a velocity of 7.2 m/s at an angle of 48![]() , the quarter lands in the cup. How high above the level where you threw the quarter does the cup sit?
, the quarter lands in the cup. How high above the level where you threw the quarter does the cup sit?
In Class Group Problem 4.7
Because of your physics background, you have been hired as a consultant for a new movie about Galileo. In one scene, he climbs up to the top of a tower and, in frustration over the people who ridicule his theories, throws a rock at a group of them standing on the ground. The rock leaves his hand at 30![]() below the horizontal. The script calls for the rock to land 15 m from the base of the tower near a group of his detractors. It is important for the script that the rock take precisely 3.0 seconds to hit the ground so that there is time for a good expressive close-up. The set coordinator is concerned that the rock will hit the ground with too much speed causing cement chips from the plaza to injure one of the high priced actors. You are told to calculate the speed of the rock hitting the ground.
below the horizontal. The script calls for the rock to land 15 m from the base of the tower near a group of his detractors. It is important for the script that the rock take precisely 3.0 seconds to hit the ground so that there is time for a good expressive close-up. The set coordinator is concerned that the rock will hit the ground with too much speed causing cement chips from the plaza to injure one of the high priced actors. You are told to calculate the speed of the rock hitting the ground.
In Class Group Problem 4.8
Because of your knowledge of physics, you have been hired as a consultant for a new James Bond movie, “Oldfinger”. In one scene, Bond jumps horizontally off the top of a cliff to escape a villain. To make the stunt more dramatic, the cliff has a horizontal ledge a distance ![]() beneath the top of the cliff which extends a distance
beneath the top of the cliff which extends a distance ![]() from the vertical face of the cliff. The stunt coordinator wants you to determine the minimum horizontal speed, in terms of
from the vertical face of the cliff. The stunt coordinator wants you to determine the minimum horizontal speed, in terms of ![]() and
and ![]() , with which Bond must jump so that he misses the edge.
, with which Bond must jump so that he misses the edge.
In Class Group Problem 4.9
Your friend has decided to make some money at the next Bristol Carnival by inventing a game of skill. In the game she has developed so far, the customer shoots a rifle at a 5.0 cm diameter target falling straight down. Anyone who hits the target in the center wins a stuffed animal. Each shot costs 50 cents. The rifle would be mounted on a pivot 1.0 meter above the ground so that it can point in any direction at any angle. When shooting, the customer stands 100 m from where the target would hit the ground if the bullet misses. At the instant the bullet leaves the rifle (with a muzzle velocity of 1200 ft/sec according to the manual) the target is released from its holder 7.0 meters above the ground. Your friend asks you to try out the game which she has set up on a farm outside of town. Before you fire the gun, calculate where you should aim.
In Class Group Problem 4.10
A dare-devil is planning to jump a narrow section of the Grand Canyon on his rocket-propelled motorcycle. He fires up the rockets (which accelerate the motorcycle in the horizontal direction) and drives towards the cliff, leaving the edge of the cliff traveling horizontal to the ground at 45 m/s. The rockets maintain a constant acceleration all the way across the canyon, and he lands 30 m horizontally and 2 m vertically below where he left the other edge of the canyon. What minimum acceleration did the rockets have to provide for him to make a successful landing on the other side?
Practice Exam Question 4.1
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
Wile E. Coyote is standing on a cliff 13 vertical meters above a canyon in which the Road Runner is napping. If the Road Runner is napping 62 horizontal meters from the bottom of the vertical cliff, how fast does Coyote need to run off the edge of the horizontal cliff to land directly on top of the Road Runner?
Practice Exam Question 4.2
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
Your friend challenges you to a go-kart race. She is driving at her constant maximum speed of 9.2 m/s when she passes you, and you are driving at 1.8 m/s as she passes. You hit the accelerator as she passes and accelerate at 0.20 m/s![]() until you pass her. How long does it take you to catch up to her?
until you pass her. How long does it take you to catch up to her?
Practice Exam Question 4.3
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
During a tournament, a golfer hits her ball off the tee at a velocity of 55 m/s at an angle of 22![]() up from the horizontal. The ball lands on the fairway 13 m below her position. How far did the ball travel horizontally (what is
up from the horizontal. The ball lands on the fairway 13 m below her position. How far did the ball travel horizontally (what is ![]() )?
)?
Practice Exam Question 4.4
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
You are watching people practicing archery when you wonder how fast an arrow is shot from a bow. With a flash of insight you remember your physics and see how you can easily determine what you want to know by a simple measurement. You ask one of the archers to pull back her bowstring as far as possible and shoot an arrow horizontally. The arrow strikes the ground at an angle of 86 degrees from the vertical at 100 feet from the archer. What was the initial velocity (magnitude and direction) of the arrow?
Practice Exam Question 4.5
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
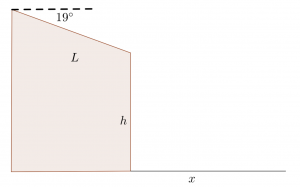
A cliff diver positions herself on a cliff that angles downwards towards the edge. The length of the top of the cliff (![]() ) is 44.0 m and the angle of the cliff is
) is 44.0 m and the angle of the cliff is ![]() = 19.0
= 19.0![]() below the horizontal. The cliff diver runs towards the edge of the cliff with a constant speed, and reaches the edge of the cliff in a time of 5.80 s. After running straight off the edge of the cliff (without jumping up), the diver falls
below the horizontal. The cliff diver runs towards the edge of the cliff with a constant speed, and reaches the edge of the cliff in a time of 5.80 s. After running straight off the edge of the cliff (without jumping up), the diver falls ![]() = 26.0 m before hitting the water. Assume there is no air friction.
= 26.0 m before hitting the water. Assume there is no air friction.
How long does it take her to hit the water after leaving the edge of the cliff?
How far does she travel horizontally (![]() ) after leaving the edge of the cliff before hitting the water?
) after leaving the edge of the cliff before hitting the water?
Practice Exam Question 4.6
These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam.
Starbuck and Apollo have landed their spaceship, a Viper, on a strangely shaped moon while looking for water. This particular moon has a sideways gravitational field with a magnitude of 7.38 m/s![]() in a direction pointing 42
in a direction pointing 42![]() down from the
down from the ![]() axis. While standing on a ledge 8.00 m above the level ground, Starbuck kicks a rock at Apollo, who is standing on the ground. The rock hits the ground at his feet. If she kicked the rock up into the air at 12.5 m/s and at an angle of 17
axis. While standing on a ledge 8.00 m above the level ground, Starbuck kicks a rock at Apollo, who is standing on the ground. The rock hits the ground at his feet. If she kicked the rock up into the air at 12.5 m/s and at an angle of 17![]() above the horizontal,
above the horizontal,
how long does it take for the rock to hit the ground at Apollo’s feet?
What is the ![]() displacement between Starbuck and Apollo?
displacement between Starbuck and Apollo?
The study of how things move. We will often refer to the 'kinematics equations', three equations that relate displacement, velocity, and acceleration in a straight line.
Things that are orthogonal are perpendicular to each other. Our coordinate systems (x,y,z/Cartesian, polar, etc.) are orthogonal systems - changing something in one direction does NOT change what's going on in the other direction.
The straight-line vector between the original and final position, given by the vector r = x + y + z.
The path along which an object moves.
An object moving under the influence of gravity, and possibly other forces.
The top of the path of a projectile under the force of gravity. The velocity in the y direction is equal to zero at the apex.

