3.2 Structure of Earth
Portions modified from "Physical Geology" by Steven Earle*
In the previous section we learned that materials in the early Earth were sorted through the process of differentiation, with denser materials like iron and nickel sinking to the center, and lighter materials (oxygen, silicon, magnesium) remaining near the surface. As a result, the Earth is composed of layers of different composition and increasing density as you move from the surface to the center (Figure 3.2.1).
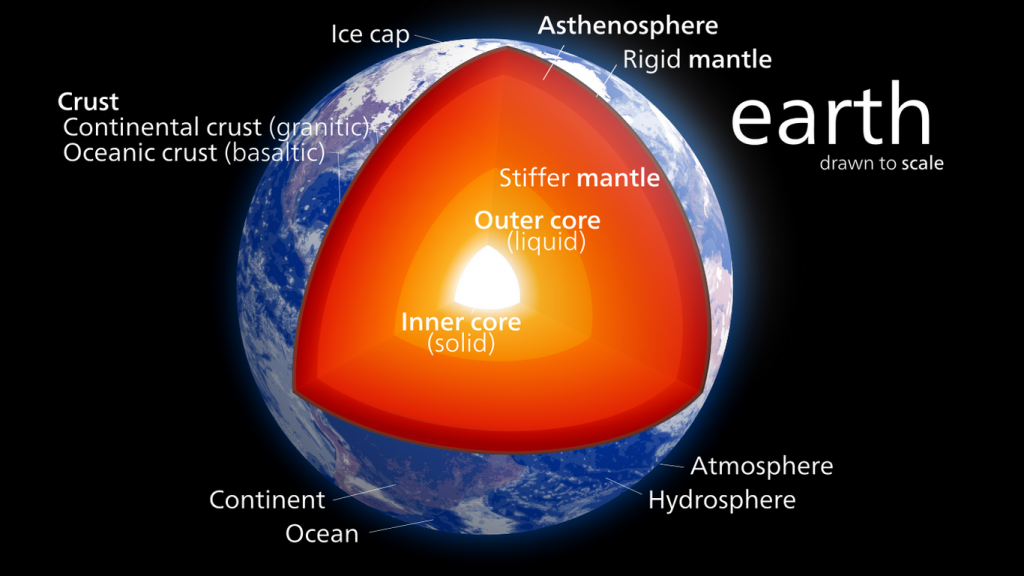
The traditional view based on chemical composition recognizes four distinct layers:
The inner core lies at the center of the Earth, and is about 1200 km thick. It is composed primarily of iron alloys and nickel, with about 10% comprised of oxygen, sulfur or hydrogen. The temperature in the inner core is about 6000 oC (10,800 oF), which is roughly the temperature of the surface of the sun (section 3.1 explains the sources of this intense heat). Despite the high temperature that should melt these metals, the extreme pressure (from literally the weight of the world) keeps the inner core in the solid phase. The solid metals also make the inner core very dense, at about 17 g/cm3, giving the inner core about one-third of the Earth’s total mass.
The outer core sits outside of the inner core. It has the same composition as the inner core, but it exists as a fluid, rather than a solid. The temperature is 4000-6000 oC, and the metals remain in the liquid state because the pressure is not as great as in the inner core. It is the movement of the fluid iron in the outer core that creates Earth’s magnetic field (see section 4.2). The outer core is 2300 km thick, and has a density of 12 g/cm3.
The mantle extends from the outer core to just under Earth’s surface. It is 2900 km thick, and contains about 80% of the Earth’s volume. The mantle consists of iron and magnesium silicates and magnesium oxides, so it is more similar to the rocks of Earth’s surface than to the materials in the core. The mantle has a density of 4.5 g/cm3, and temperatures in the range of 1000-1500 oC. The uppermost layer of the mantle is more rigid, while the deeper regions are fluid, and it is the motion of fluid materials in the mantle that is responsible for plate tectonics (see section 4.3). Magma that rises to the surface through volcanoes originates in the mantle.
The outermost layer is the crust, which forms the solid, rocky surface of the Earth. The crust averages 15-20 km thick, but in some places, such as under mountains, the crust can reach thicknesses of up to 100 km. There are two main types of crust; continental crust and oceanic crust that differ in a number of ways. Continental crust is thicker than oceanic crust, averaging 20-70 km thick, compared to 5-10 km for oceanic crust. Continental crust is also older than oceanic crust; the oldest rocks in continental crust are about 4.4 billion years old, while the oldest oceanic crust only goes back about 180 million years. Finally, the two types of crust differ in their composition. Continental crust is made largely of granite, while oceanic crust is mostly composed of basalt. Basalt contains a higher proportion of heavier elements like iron and magnesium, making oceanic crust denser than continental crust (3 g/cm3 vs. 2.7 g/cm3.) Granite also contains larger crystals than basalt, as underground or surface continental magmas can cool slowly, which allows time for crystal structures to form before the rocks solidify. Basalt also forms from cooling magmas, but exposure to air or water can cause them to cool faster, which does not allow time for large crystals to form.
Based on physical characteristics, we can also divide the outermost layers of Earth into the lithosphere and asthenosphere. The lithosphere consists of the crust and the cool, rigid, outer 80-100 km of the mantle. The crust and outer mantle moves together as a unit, so they are combined together into the lithosphere. The asthenosphere lies below the lithosphere, from about 100-200 km to about 670 km deep. It includes the more “plastic” softer region of the mantle, where fluid movements can occur. The solid lithosphere is thus floating on the fluid asthenosphere.
Isostasy
To help explain how the lithosphere is floating on the asthenosphere, we need to examine the concept of isostasy. Isostasy refers to the way a solid will float on a fluid. The relationship between the crust and the mantle is illustrated in Figure 3.2.2. On the right is an example of a non-isostatic relationship between a raft and solid concrete. It’s possible to load the raft up with lots of people, and it still won’t sink into the concrete. On the left, the relationship is an isostatic one between two different rafts and a swimming pool full of peanut butter. With only one person on board, the raft floats high in the peanut butter, but with three people, it sinks dangerously low. We’re using peanut butter here, rather than water, because its viscosity more closely represents the relationship between the crust and the mantle. Although it has about the same density as water, peanut butter is much more viscous (stiff), and so although the three-person raft will sink into the peanut butter, it will do so quite slowly.

The relationship of Earth’s crust to the mantle is similar to the relationship of the rafts to the peanut butter. The raft with one person on it floats comfortably high. Even with three people on it the raft is less dense than the peanut butter, so it floats, but it floats uncomfortably low for those three people. The crust, with an average density of around 2.6 grams per cubic centimeter (g/cm3), is less dense than the mantle (average density of approximately 3.4 g/cm3 near the surface, but more than that at depth), and so it is floating on the “plastic” mantle. When more weight is added to the crust, through the process of mountain building, it slowly sinks deeper into the mantle and the mantle material that was there is pushed aside (Figure 3.2.3, left). When that weight is removed by erosion over tens of millions of years, the crust rebounds and the mantle rock flows back (Figure 3.2.3, right).
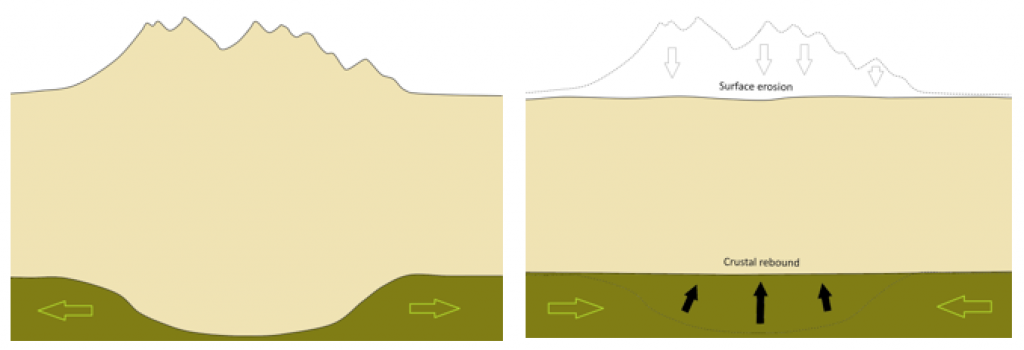
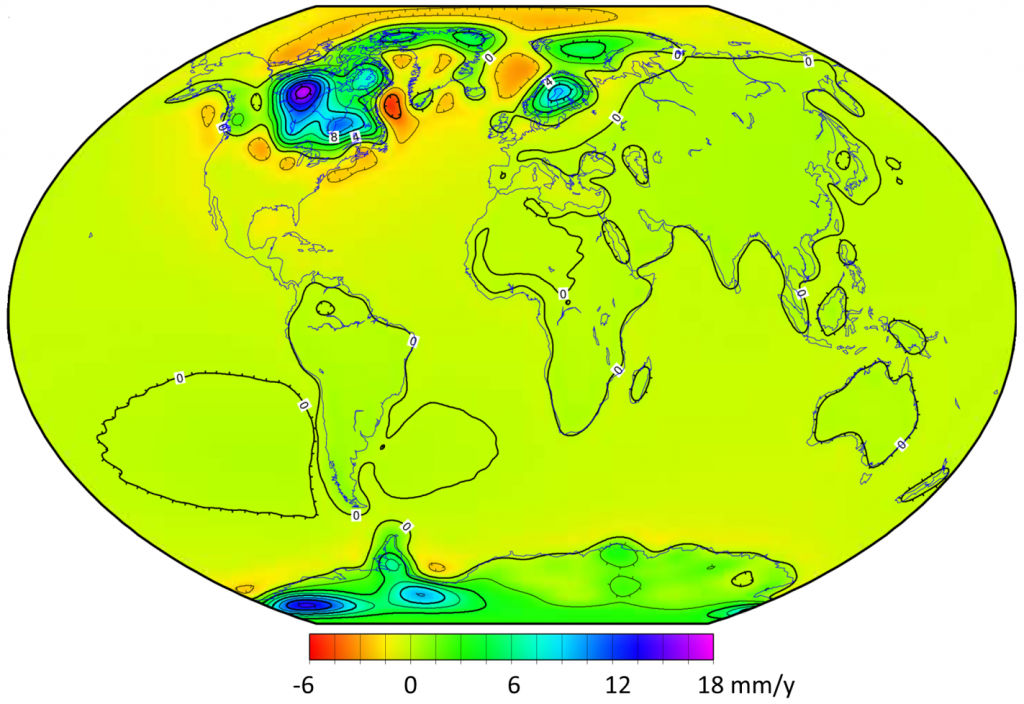
The crust and mantle respond in a similar way to glaciation. Thick accumulations of glacial ice add weight to the crust, and as the mantle beneath is squeezed to the sides, the crust subsides. When the ice eventually melts, the crust and mantle will slowly rebound, but full rebound will likely take more than 10,000 years. Large parts of Canada are still rebounding as a result of the loss of glacial ice over the past 12,000 years, and as shown in Figure 3.2.4, other parts of the world are also experiencing isostatic rebound. The highest rate of uplift is in within a large area to the west of Hudson Bay, which is where the Laurentide Ice Sheet was the thickest (over 3,000 m). Ice finally left this region around 8,000 years ago, and the crust is currently rebounding at a rate of nearly 2 cm/year.
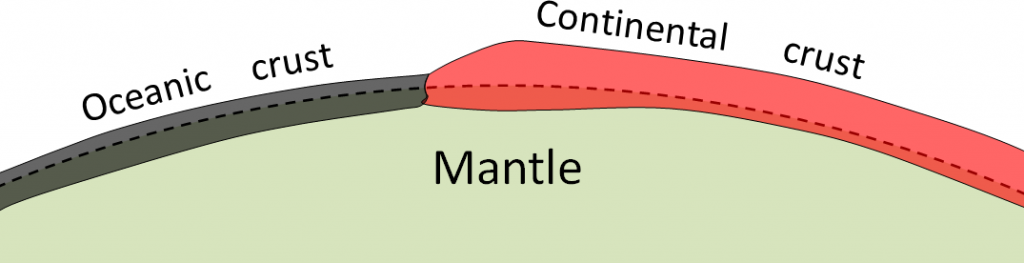
Since continental crust is thicker than oceanic crust, it will float higher and extend deeper into the mantle than oceanic crust. The boundary between the crust and the mantle is known as the Mohorovičić discontinuity (or Moho; see section 3.3). Crust is thickest where there are mountains, so the Moho will be deeper under mountains than under the oceanic crust. Since oceanic crust is also denser than continental crust, it floats lower on the mantle. Since the oceanic crust lies lower than the continental crust, and since water flows downhill to reach the lowest point, this explains why water has accumulated over the oceanic crust to form the oceans.
*”Physical Geology” by Steven Earle used under a CC-BY 4.0 international license. Download this book for free at http://open.bccampus.ca
the un-mixing of a magma, typically by the physical separation of minerals that crystallize early and settle towards the bottom (3.1)
mass per unit volume of a substance (e.g., g/cubic cm) (6.3)
the solid metal mass at the center of the Earth, extending 1200 km from the center (3.2)
the layer of the inner Earth extending 2300 km from the top of the inner core to the bottom of the mantle, composed of fluid metal alloys (3.2)
the middle layer of the Earth, dominated by iron and magnesium rich silicate minerals and extending for about 2900 km from the base of the crust to the top of the core (3.2)
the uppermost layer of the Earth, ranging in thickness from about 5 km (in the oceans) to over 50 km (on the continents) (3.2)
the Earth’s crust underlying the continents (as opposed to ocean crust) (3.2)
the Earth’s crust underlying the oceans (as opposed to continental crust) (3.2)
an igneous (formed from cooling magma) rock that comprises much of the continental crust (3.2)
a volcanic rock that makes up much of the oceanic crust (3.2)
the rigid outer part of the Earth, including the crust and the mantle down to a depth of about 100 km (3.2)
the part of the mantle, from about 100 to 200 km below surface, within which the mantle material is close to its melting point, and therefore relatively weak (3.2)
the equilibrium position reached by a block of crust floating on the underlying fluid mantle (3.2)
the continental glacier that extended across central eastern North America during the Pleistocene, covering most of Canada and a significant part of the United States (3.2)
the boundary between the crust and the mantle (3.3)

