6.3 Density
Density refers to the amount of mass per unit volume, such as grams per cubic centimeter (g/cm3). The density of fresh water is 1 g/cm3 at 4o C (see section 5.1), but the addition of salts and other dissolved substances increases surface seawater density to between 1.02 and 1.03 g/cm3. The density of seawater can be increased by reducing its temperature, increasing its salinity, or increasing the pressure. Pressure has the least impact on density as water is fairly incompressible, so pressure effects are not very significant except at extreme depths. However, if not for the slight compression of water due to pressure, sea level would be approximately 50 m higher than it is today! That leaves temperature and salinity as the primary factors determining density, and of these, temperature has the greatest impact (Figure 6.3.1).
Since temperature has the greatest effect on density, density profiles are usually mirror images of temperature profiles (Figure 6.3.2). Density is lowest at the surface, where the water is the warmest. As depth increases, there is a region of rapidly increasing density with increasing depth, which is called the pycnocline. The pycnocline coincides with the thermocline, as it is the sudden decrease in temperature that leads to the increase in density. Below the pycnocline, density may be fairly constant (as is temperature), or it may continue to increase slightly towards the bottom.
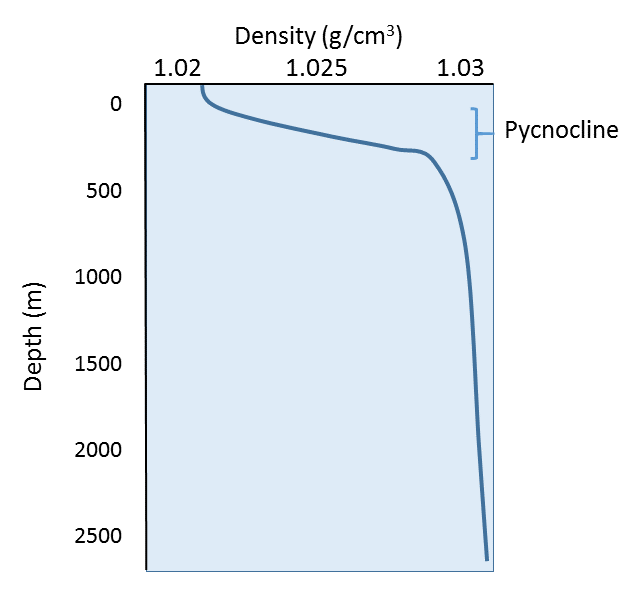
The profile above represents a stable state, or a high degree of stratification, where the warm, low density layer sits atop the colder, denser layer. If denser water happened to form at the surface, the water masses would be unstable, and the denser water would sink to the bottom, to be replaced by less dense water at the surface. This vertical movement of water masses based on density (as determined by temperature and salinity) is referred to as thermohaline circulation, which is the topic of section 9.8. By creating a stratified water column, the thermocline and pycnocline together create a barrier that prevents mixing between the warmer, less dense surface water and the colder, denser bottom water. In this way, nutrient-rich deep water may be prevented from coming to the surface to support primary production.
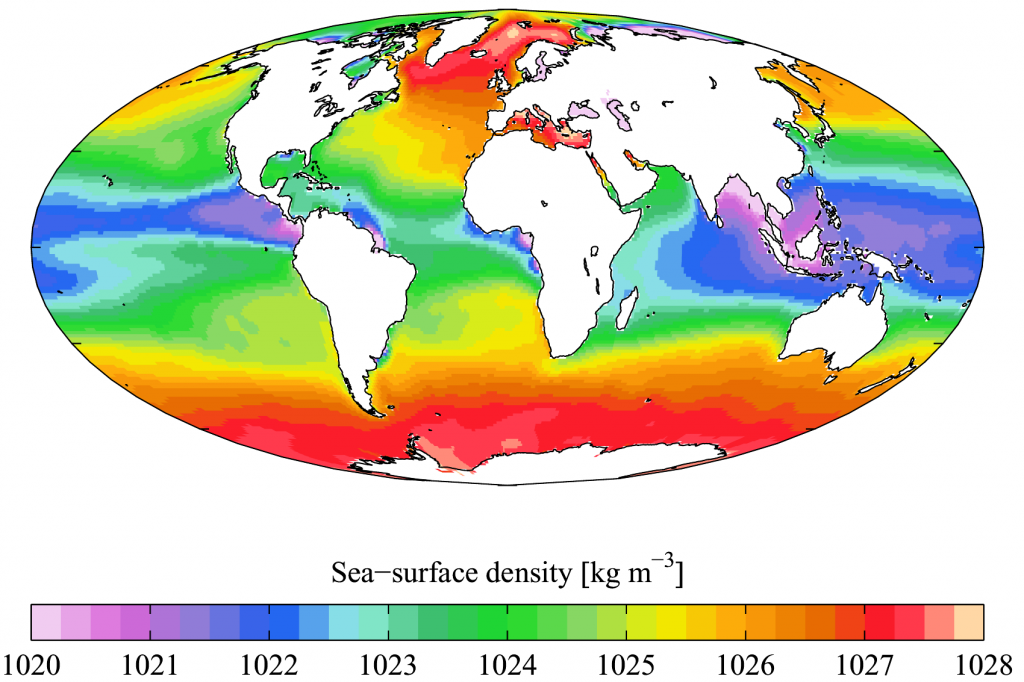
As with temperature, there are also latitudinal differences in density. In the tropics the surface water is warm and low density, and there is a pronounced thermocline separating it from the colder, denser deep water. As stated above, this stratification prevents nutrient-rich water from reaching the surface and as a result tropical regions often have low productivity. In the high latitudes the water is uniformly cold at all depths, so there is little density stratification. The lack of a pycnocline (or a thermocline) allows cold, nutrient-rich deep water to more easily mix with the surface water, leading to higher primary production in polar regions.
the concentration of dissolved ions in water (5.3)
a region in the water column where there is a large change in density over a small change in depth (6.3)
a region in the water column where there is a dramatic change in temperature over a small change in depth (6.2)
deep ocean circulation driven by differences in water density (9.8)
the synthesis of organic compounds from aqueous carbon dioxide by plants, algae, and bacteria (7.1)

