3.3 Determining the Structure of Earth
Modified from "Physical Geology" by Steven Earle*
The previous section described the properties and composition of Earth’s interior, which begs the question: how can we know what conditions are like deep in the Earth? It’s easy to sample the crust through drilling, and mantle material often comes to the surface as magma, but the farthest we have been able to drill into the crust so far is only about 12 km; this for a planet with a radius of 6370 km! So to understand the composition and structure of the Earth’s deep interior, we need to use indirect methods such as seismology.
Seismology is the study of vibrations within the Earth. These vibrations are caused by various events, including earthquakes, extraterrestrial impacts, explosions, storm waves hitting the shore, and tidal effects. Of course, seismic techniques have been most widely applied to the detection and study of earthquakes, but there are many other applications, and arguably seismic waves provide the most important information that we have concerning Earth’s interior. Before going any deeper into Earth, however, we need to take a look at the properties of seismic waves. The types of waves that are useful for understanding Earth’s interior are called body waves, meaning that, unlike the surface waves on the ocean, they are transmitted through Earth materials.
Imagine hitting a large block of strong rock (e.g., granite) with a heavy sledgehammer. At the point where the hammer strikes it, a small part of the rock will be compressed by a fraction of a millimeter. That compression will transfer to the neighboring part of the rock, and so on through to the far side of the rock, from where it will bounce back to the top — all in a fraction of a second. This is known as a compression wave, and it can be illustrated by holding a loose spring (like a Slinky) that is attached to something (or someone) at the other end. If you give it a sharp push so the coils are compressed, the compression propagates (travels) along the length of the spring and back (Fig. 3.3.1). You can think of a compression wave as a “push” wave — it’s called a P-wave (although the “P” stands for “primary” because P-waves are the first to arrive at seismic stations). In a P-wave the motion of the particles is parallel to the direction of wave propagation.
When we hit a rock with a hammer, we also create a different type of body wave, one that is characterized by back-and-forth vibrations (as opposed to compressions). This is known as a shear wave (S-wave, where the “S” stands for “secondary”), and an analogy would be what happens when you flick a length of rope with an up-and-down motion. As shown in Figure 3.3.1, a wave will form in the rope, which will travel to the end of the rope and back. In this case, the motion of the particles is perpendicular to the direction the wave travels.
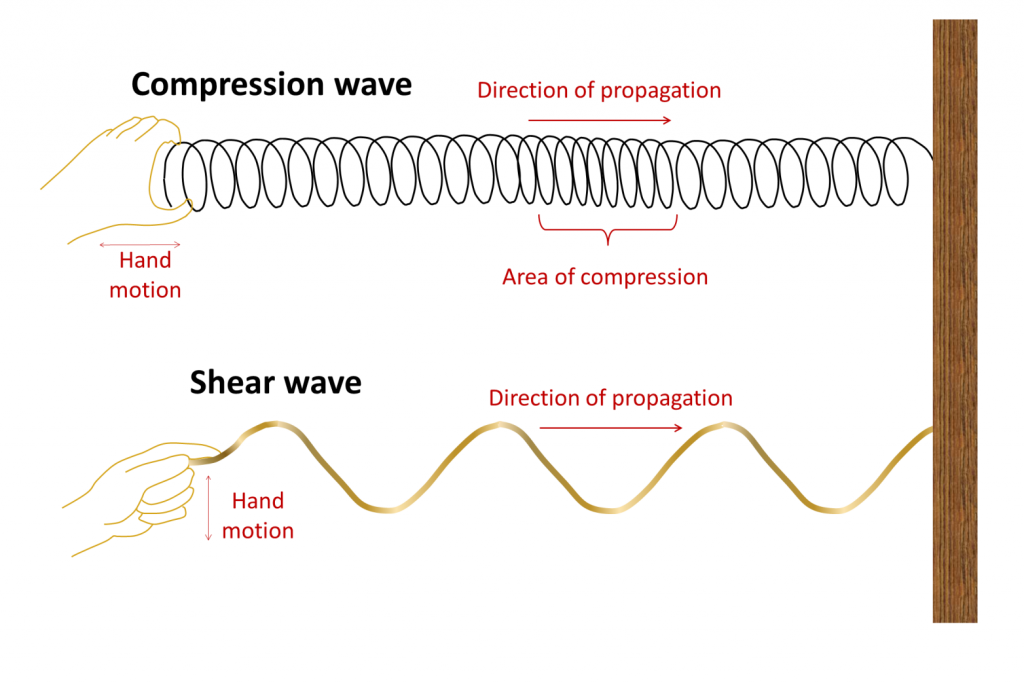
Compression waves and shear waves travel very quickly through geological materials. As shown in Figure 3.2.2, typical P-wave velocities are between 0.5 km/s and 2.5 km/s in unconsolidated sediments, and between 3.0 km/s and 6.5 km/s in solid crustal rocks. Of the common rocks of the crust, velocities are greatest in basalt and granite. S-waves are slower than P-waves, with velocities between 0.1 km/s and 0.8 km/s in soft sediments, and between 1.5 km/s and 3.8 km/s in solid rocks.
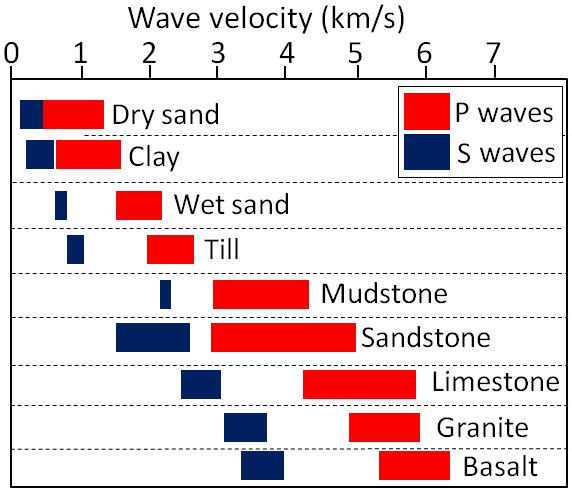
Mantle rock is generally denser and stronger than crustal rock and both P- and S-waves travel faster through the mantle than they do through the crust. Moreover, seismic-wave velocities are related to how tightly compressed a rock is, and the level of compression increases dramatically with depth. Finally, seismic waves are affected by the phase state of rock. They are slowed if there is any degree of melting in the rock. If the material is completely liquid, P-waves are slowed dramatically and S-waves are stopped altogether.
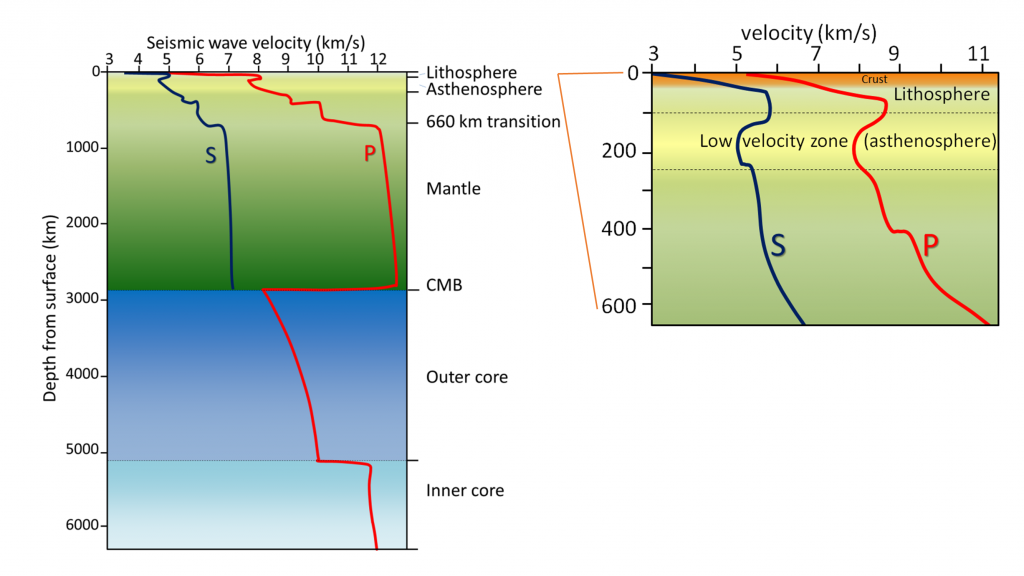
Accurate seismometers have been used for earthquake studies since the late 1800s, and systematic use of seismic data to understand Earth’s interior started in the early 1900s. The rate of change of seismic waves with depth in the Earth (Fig. 3.3.3) has been determined over the past several decades by analyzing seismic signals from large earthquakes at seismic stations around the world. Small differences in arrival time of signals at different locations have been interpreted to show that:
- Velocities are greater in mantle rock than in the crust.
- Velocities generally increase with pressure, and therefore with depth.
- Velocities slow in the area between 100 km and 250 km depth (called the “low-velocity zone”; equivalent to the asthenosphere).
- Velocities increase dramatically at 660 km depth (because of a mineralogical transition).
- Velocities slow in the region just above the core-mantle boundary (the D” layer or “ultra-low-velocity zone”).
- S-waves do not pass through the outer part of the core.
- P-wave velocities increase dramatically at the boundary between the liquid outer core and the solid inner core.
One of the first discoveries about Earth’s interior made through seismology was in the early 1900s when Croatian seismologist Andrija Mohorovičić (pronounced Moho-ro-vi-chich) realized that at certain distances from an earthquake, two separate sets of seismic waves arrived at a seismic station within a few seconds of each other. He reasoned that the waves that went down into the mantle, traveled through the mantle, and then were bent upward back into the crust, reached the seismic station first because although they had farther to go, they traveled faster through mantle rock (as shown in Figure 3.3.4). The boundary between the crust and the mantle is known as the Mohorovičić discontinuity (or Moho). Its depth is between 60 km and 80 km beneath major mountain ranges, around 30 km to 50 km beneath most of the continental crust, and between 5 km and 10 km beneath the oceanic crust.
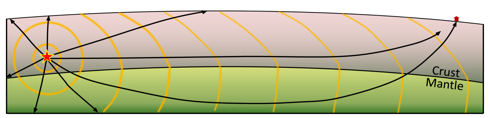
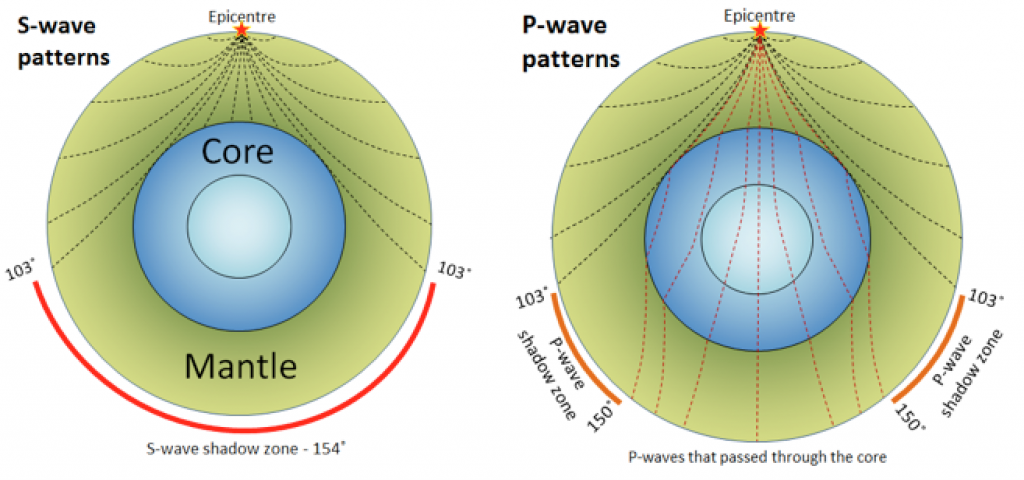
Our current understanding of the patterns of seismic wave transmission through Earth is summarized in Figure 3.3.5. Because of the gradual increase in density with depth, all waves are refracted toward the lower density, slower velocity material as they travel through homogenous parts of Earth, and thus tend to curve outward toward the surface. Waves are also refracted at boundaries within Earth, such as at the Moho, at the core-mantle boundary (CMB), and at the outer-core/inner-core boundary. S-waves do not travel through liquids — they are stopped at the CMB — and there is an S-wave shadow on the side of Earth opposite a seismic source. The angular distance from the seismic source to the shadow zone is 103° on either side, so the total angular distance of the shadow zone is 154°. We can use this information to infer the depth to the CMB. P-waves do travel through liquids, so they can make it through the liquid part of the core. Because of the refraction that takes place at the CMB, waves that travel through the core are bent away from the surface, and this creates a P-wave shadow zone on either side, from 103° to 150°. This information can be used to discover the differences between the inner and outer parts of the core.
Using data from many seismometers and hundreds of earthquakes, it is possible to create a two- or three-dimensional image of the seismic properties of part of the mantle. This technique is known as seismic tomography, and an example of the result is shown in Figure 3.3.6.
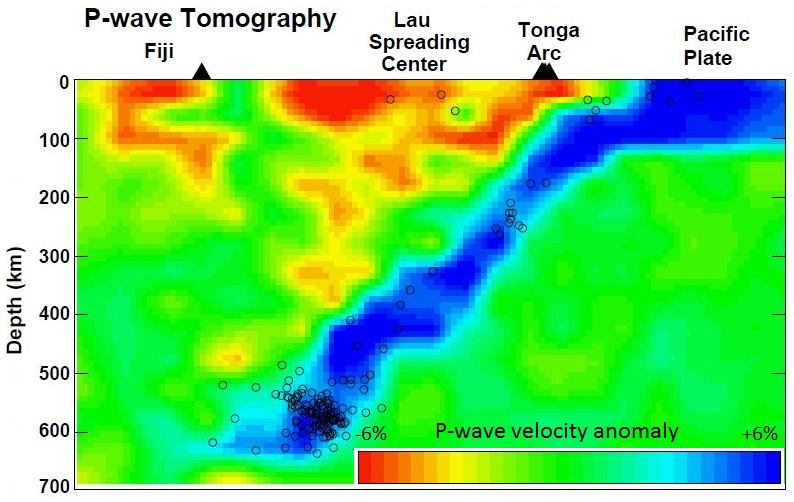
The Pacific Plate subducts beneath Tonga and appears in Figure 3.3.6 as a 100 km thick slab of cold (blue-colored) oceanic crust that has pushed down into the surrounding hot mantle. The cold rock is more rigid than the surrounding hot mantle rock, so it is characterized by slightly faster seismic velocities. There is volcanism in the Lau spreading center and also in the Fiji area, and the warm rock in these areas has slower seismic velocities (yellow and red colors).
Seismic waves provide us with the structure of the inner Earth, but what about it’s other properties? In terms of composition, there are several lines of evidence pointing to a core composed mostly of iron and nickel. Wave properties suggest the core is composed of an element with an atomic number around 25 (iron has an atomic number of 26). Aside from iron, all of the other elements with an atomic number close to 25 are too rare to make up the core. If the Earth was formed through the accretion of smaller bodies such as meteorites, we would expect the composition of Earth to be similar to the composition of meteorites. Meteorites are mostly iron and nickel, but in higher proportions than the Earth’s crust. This suggests that most of this heavy iron and nickel from the meteorites must have sunk to the Earth’s center as the planet was forming. However, the core is not dense enough to be pure iron and nickel; it it about 10% below the predicted density if that was the case. This is why scientists believe the core is composed of about 10% sulfur, oxygen, and hydrogen. Finally, if the Earth’s magnetic field comes from the fluid outer core, the outer core must contain iron. In terms of the temperatures, we can calculate the melting points of these materials over the range of pressures that they would experience in the inner Earth, and then infer the temperatures that would allow these elements to exist in their solid or liquid forms.
*”Physical Geology” by Steven Earle used under a CC-BY 4.0 international license. Download this book for free at http://open.bccampus.ca
the uppermost layer of the Earth, ranging in thickness from about 5 km (in the oceans) to over 50 km (on the continents) (3.2)
the middle layer of the Earth, dominated by iron and magnesium rich silicate minerals and extending for about 2900 km from the base of the crust to the top of the core (3.2)
the study of vibrations within the Earth (3.3)
a seismic wave that travels through rock (e.g., a P-wave or an S-wave) (3.3)
an igneous (formed from cooling magma) rock that comprises much of the continental crust (3.2)
a seismic body wave that is characterized by deformation of the rock in the same direction that the wave is propagating (compressional vibration) (3.3)
a seismic body wave that is characterized by deformation of the rock perpendicular to the direction that the wave is propagating (3.3)
a volcanic rock that makes up much of the oceanic crust (3.2)
unconsolidated particles of mineral or rock that settle to the seafloor (12.1)
the change of state between a solid, liquid, or gas (8.1)
the part of the mantle, from about 100 to 200 km below surface, within which the mantle material is close to its melting point, and therefore relatively weak (3.2)
the metallic interior part of the Earth, extending from a depth of 2900 km to the center (3.2)
the layer of the inner Earth extending 2300 km from the top of the inner core to the bottom of the mantle, composed of fluid metal alloys (3.2)
the solid metal mass at the center of the Earth, extending 1200 km from the center (3.2)
the boundary between the crust and the mantle (3.3)
mass per unit volume of a substance (e.g., g/cubic cm) (6.3)
when part of a plate is forced beneath another plate along a subduction zone (4.3)
the Earth’s crust underlying the oceans (as opposed to continental crust) (3.2)
the process by which solid celestial bodies are added to existing bodies during collisions (3.1)
a fragment of either stony or metallic debris in space (12.5)

